今回の記事は前回からの続きになります。 前回の記事はこちら↓
前回は光電効果という現象がこれまで知られていた物理ではまったく説明できないというところまで解説しました。
この謎がどのように解明されたのか。
解決編,スタートです。
天才,現る
当時の物理学者が光電効果の不可思議な性質に頭を悩ませていたとき,物理界に颯爽と現れ(たかどうかは定かではないが笑),華麗に解決してしまったのが,かの有名なアインシュタインです!
光電効果を解決するためにアインシュタインが主張したのはただ1つ。
「光電効果において,光は粒子として振る舞っている」
ただこれだけ。
当時の人々「…は?」
アインシュタインの光量子仮説
アインシュタインの主張をちゃんと書くと,「光が粒子としての性質をもっていると考えれば,光電効果はうまく説明できる。」です。
ここで勘違いしないでほしいのが,アインシュタインは「光が波である」ことを否定していないこと。
光=電磁波はすでにマクスウェルによって示されているので,否定のしようがありません。
つまり,アインシュタインは「光は波であるが,粒子のようにも振る舞う」と言っているのです!
…これを読んで「ふーん」とか思ってる人は甘い! もっと驚け!
アインシュタインのこの提唱は正直信じ難いものです。
なぜなら大昔から,粒子と波は相反するものだと考えられていたから。
(粒子は衝突すればはねかえるが,波は衝突しても独立性によりそのまま進むなど,粒子のもつ性質と波のもつ性質は相容れない。)
その常識を無視してアインシュタインは,
「光は粒子として振る舞うよ。え? あぁ,もちろん光は電磁波だけどね!」
と訳のわからない主張をしたわけです。
いくら訳がわからなくても,実験結果をちゃんと矛盾なく説明できれば万事OK。
実際,この常識破りのアイデアから新たな物理が幕を開けることになります。 これが天才ってやつか。
話が逸れてきたので本題に戻りましょう。
アインシュタインのこの主張は,正式には「光量子(こうりょうし)仮説」と呼ばれています。
光がこのような性質をもつとすれば,謎だらけだった光電効果がすべて説明できます!
光電効果の解決
ここで前回まとめた光電効果の性質をもう一度おさらいしましょう。
まず簡単な③の性質から。 これは光量子仮説(ⅰ)によって説明可能。
光を粒だとして,1個の光子のエネルギーが,1個の電子に受け渡されるとすると,光子の数が多い(=強い光)ほどたくさんの電子にエネルギーを与え,光電子にすることができます。
次に②の性質。 これは光量子仮説(ⅱ)によって説明可能。
ここで大事なのは,「光の強さ」と「光子のエネルギー」の2つを明確に区別すること。
言葉のイメージだとどうしても「強い=エネルギーが大きい」とイメージしがちですが,それは間違い!!
上で書いたことの繰り返しになりますが,
・光の強さ = 光子の数
・光子のエネルギー = hν
です。
なので,光子の数が多くても振動数が小さければ,それは “強いけどエネルギーが小さい光” になります。
強さとエネルギーは決してイコールではありません。
(※ 可視光線なら強い光は明るく見え,エネルギーの高い光は青や紫色に見える。)
これを踏まえた上で,光電効果②の性質を見てみましょう。
光子が電子に与えるエネルギーは光の振動数で決まる(E=hν)ため,光の振動数が大きければ光電子の運動エネルギーも必然的に大きくなります。
が,光を強くしても光子の数が増えるだけで,光子のエネルギーは変化しません。
よって,光の強さを変えても光電子のエネルギーに変化は起こらないのです。
最後に性質①。
これも光量子仮説(ⅱ)によって説明可能ですが,その前に金属内の自由電子について考察しましょう。
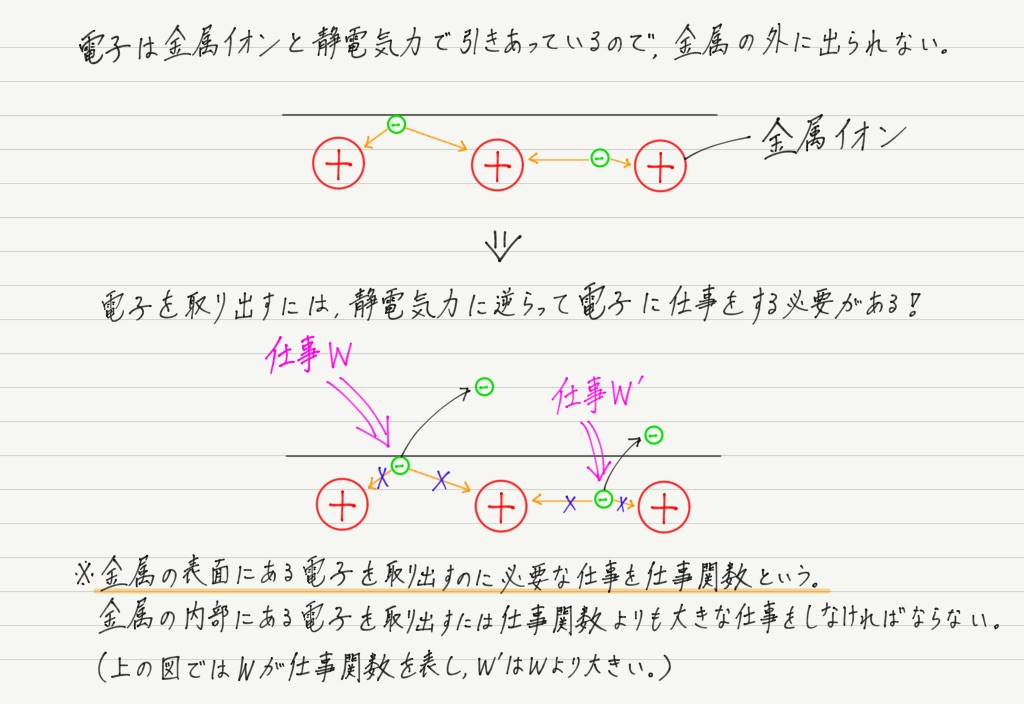
自由電子は金属の陽イオンから引力を受けているので,金属の外に飛び出すことはありません。
つまり,電子を金属から引き剥がしたければ,外部からエネルギーを加える(仕事をする)必要があります!
(※ 仕事関数の値は金属の種類によって異なる。)
以上のことが理解できていれば,性質①も理解できるはずです。
光子が元々もっていたエネルギーhνは,まず自由電子を金属表面から引き剥がす仕事に使われます。
しかし光の振動数が小さく,光子のエネルギーが十分でなければ電子を金属表面から引き剥がすことができず,光電効果は起こりません!
これが限界振動数の正体です。
一方で限界振動数よりも大きい振動数の光を照射すれば,ただちに電子は金属から引き剥がされます。
そして,引き剥がして余ったエネルギーが光電子の運動エネルギーになるのです(性質②)。
光=電磁波説ではまったく説明できなかった光電効果ですが,光量子仮説を採用すればこのように簡単に説明できます!
アインシュタインすげー。
光電効果の式とグラフ
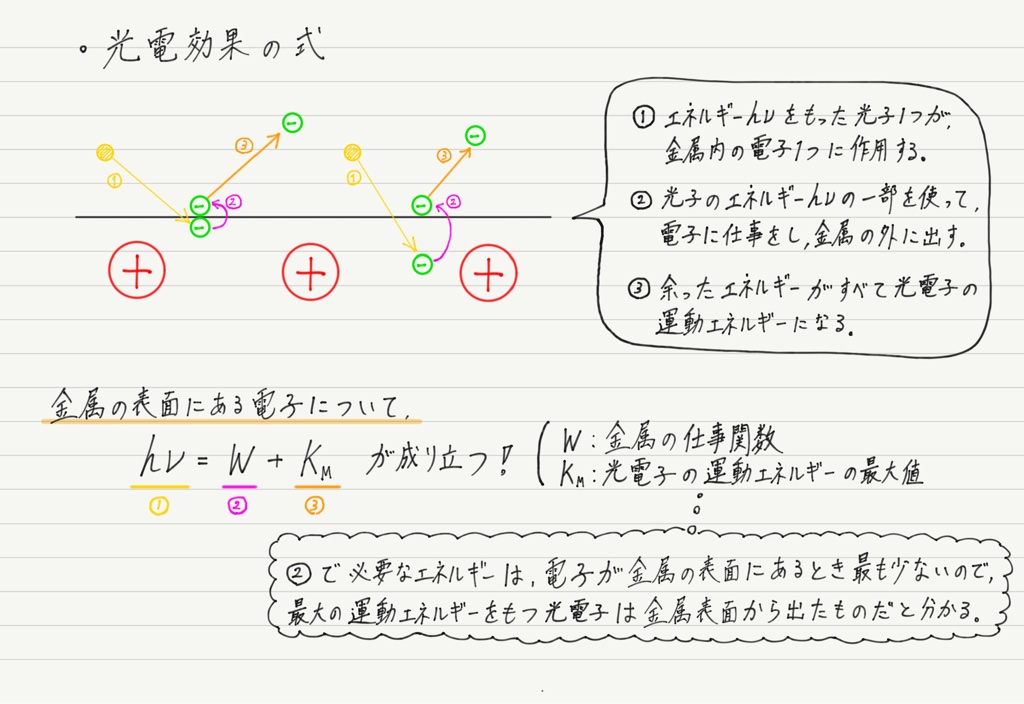
光電効果の性質①の説明を式の形に直してみましょう。
この式はあくまでも,“金属表面にあった電子” についての式だということに注意してください。
金属内部にあった電子は仕事が最小でもなければ運動エネルギーが最大でもなく,扱いようがありません。
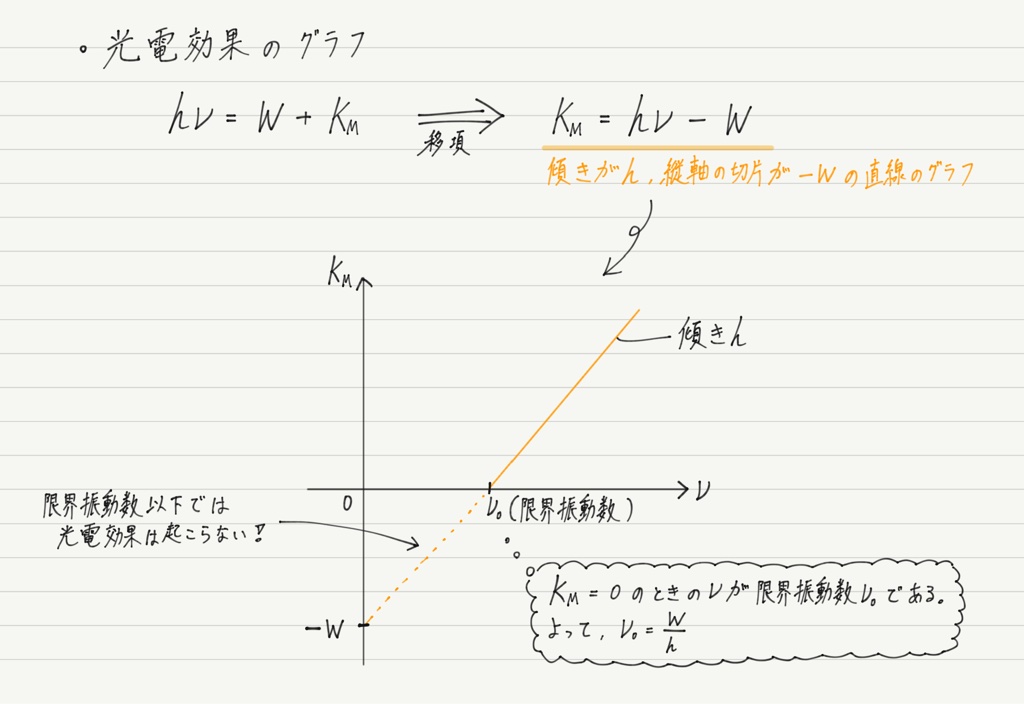
式を求めたついでに,縦軸に光電子の運動エネルギー(の最大値),横軸に光の振動数をとってグラフをつくってみましょう。
グラフの傾き・縦軸の切片・横軸の切片がそれぞれ,プランク定数・仕事関数・限界振動数という光電効果で重要な値をそれぞれ表していて,興味深いグラフですね!
今回のまとめノート
ちなみに,アインシュタインはこの光電効果の解明を理由にノーベル物理学賞を受賞しています。
アインシュタインの業績でいちばん有名なのは相対性理論ですが,そっちでは受賞していないというね笑
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回はレントゲンでおなじみ,X線について学んでいきます。