今回はファラデーの電磁誘導の法則が具体的な回路でどのように使われるかを，典型問題を例にとって見ていきましょう！
例題
電磁誘導でもっともよく出題されるのがこのタイプの問題。 しっかり解けるようにしておきたいところです。
解答・解説
ではさっそく解説へ。 今回の問題で注意すべきポイントは，
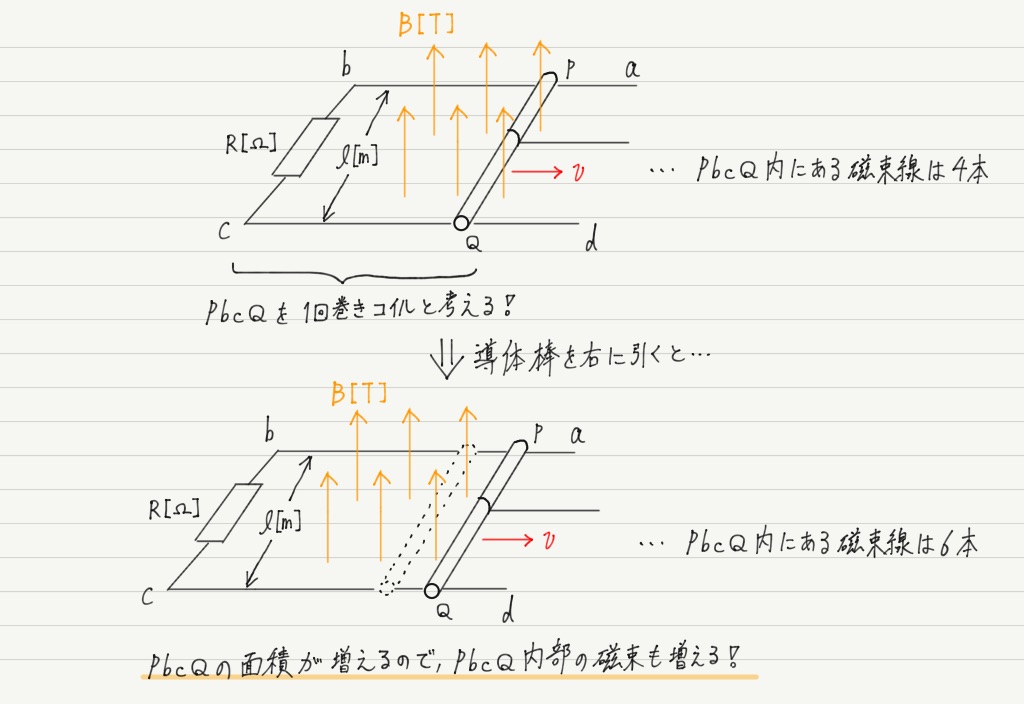
・「回路 ＝ 1回巻きのコイル」とみなすこと
・磁束密度は変化しないが，棒が磁場を横切ることで磁束線が貫く面積が変化すること
の2点です。 この2点を合わせて考えると，回路に誘導起電力が生じることがわかります。 図で説明すると，
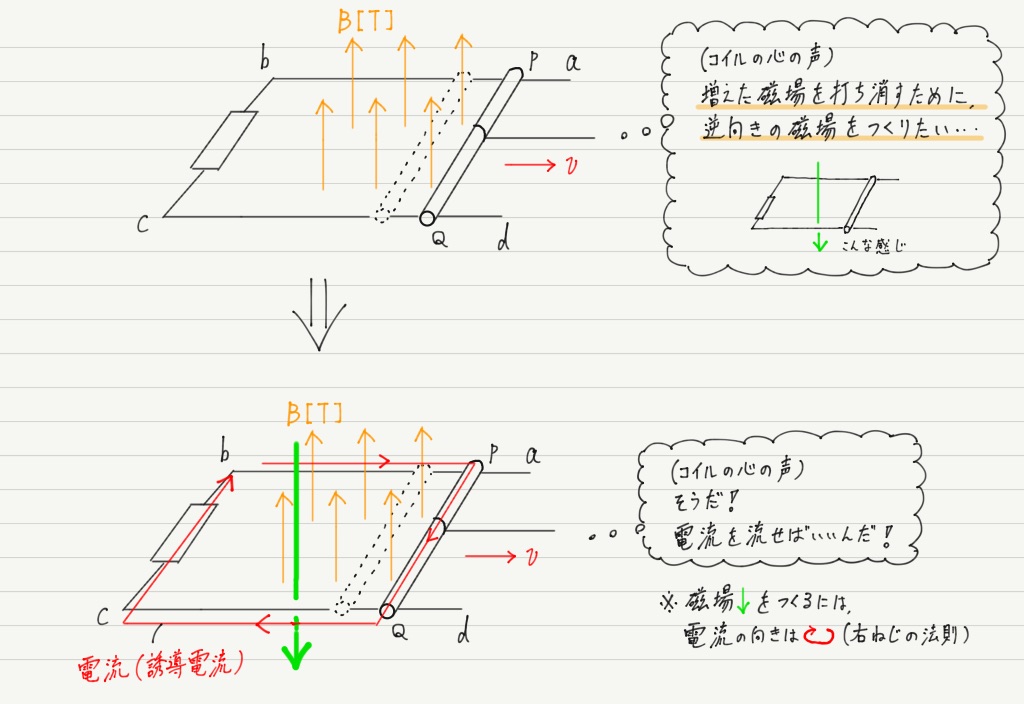
コイル内部の磁束が増えると，コイルはあまのじゃくなので，誘導電流をつくって磁束を減らそうとします！（レンツの法則＆右ねじの法則！）
この説明がピンとこない人は過去記事で要復習↓ ↓ ↓
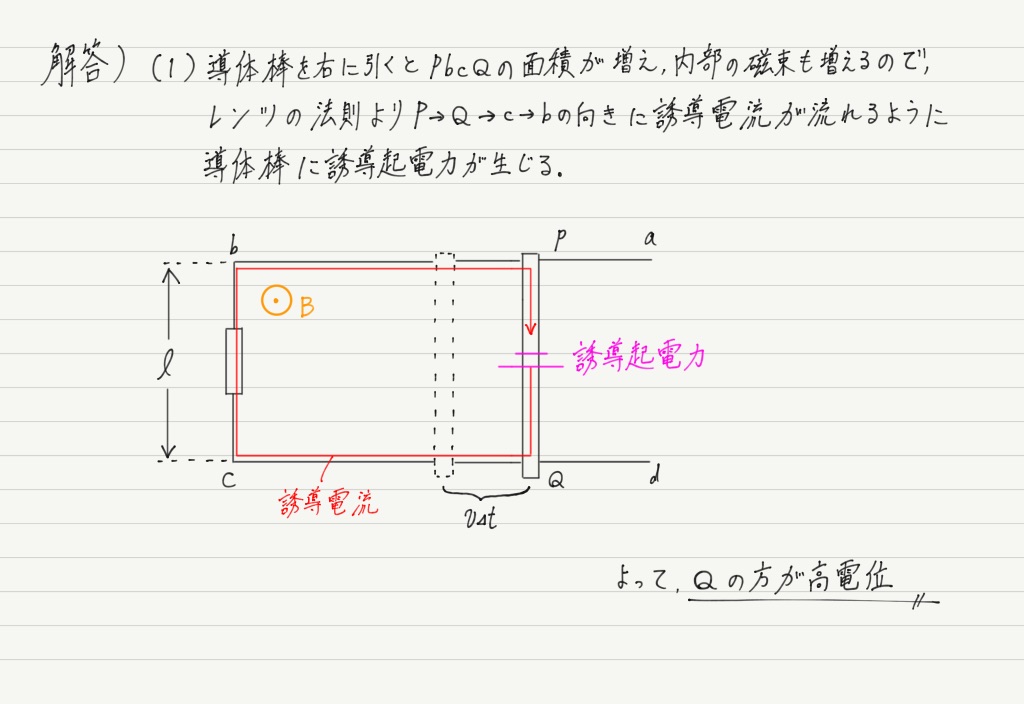
さぁ，回路に誘導電流が流れることがわかったので，これをヒントに解いていけばよさそうです！
前回の記事でお伝えしたセオリーどおり，誘導起電力の向きと大きさは別々に考えていきましょう。
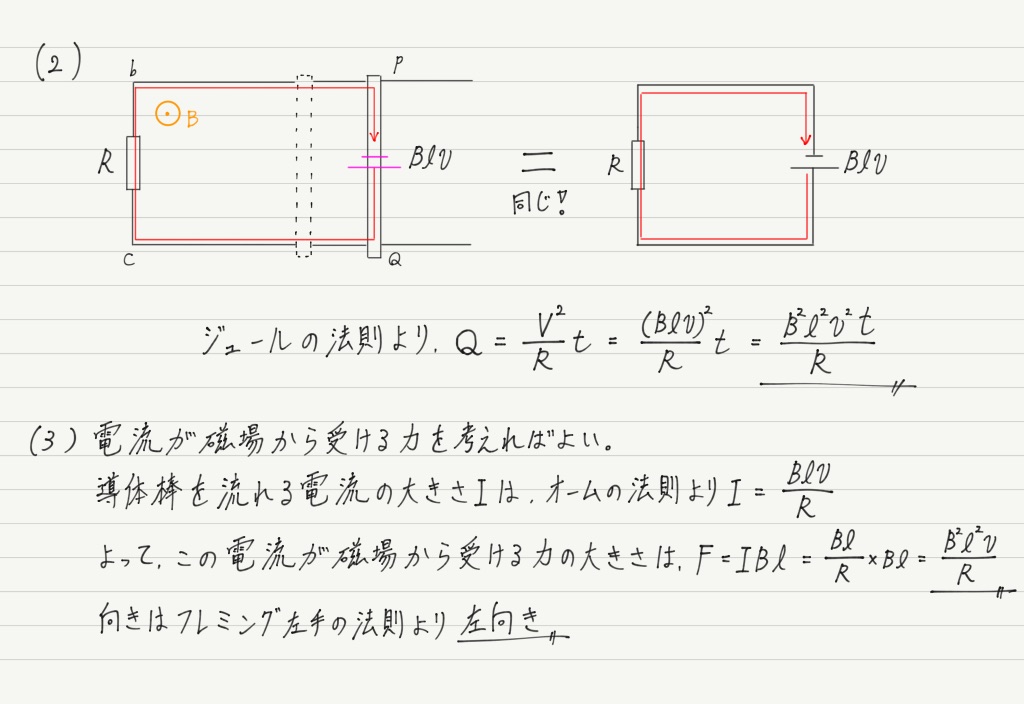
このV = Blvという結果は，教科書では半ば公式として扱われていますが，実際はいまの計算のように，ファラデーの電磁誘導の法則から得られる式です。 公式として覚えることは否定しませんが，自分で導けるようになっておくと応用力もUPします！
…さて，今回のテーマは電磁誘導の問題を解こう！なのですが，電磁誘導が登場するのは（1）だけ。
（1）で導体棒に生じる誘導起電力Vが求められたので，（2）以降は導体棒を電池だと考えればOK。
電流が磁場から受ける力の公式を忘れてしまっている人がいたら，これを機に思い出しておきましょう。 では最後に（4）。
解答にひとつだけ補足。（3）で力の向きを求めましたが，コイルの性質を考えれば，フレミング左手の法則を使わずに求められます。
コイルの性質は何といっても “あまのじゃく” なところ。 誰かが導体棒を右に引っ張ったら，あまのじゃくなコイルは左に引き戻そうとするはずです。 だから力の向きは左。
ね？ 簡単でしょ？ 今回はここまで。
解説のために簡単な例題を扱いましたが，磁場を横切る導体棒の問題はさまざまなバリエーションがあるので，ぜひ各自でチャレンジしてみてください！
おまけ：動けばいいってもんじゃない
ここでまちがい探しをしてみましょう。 以下の文章を読んで，まちがいを見つけてみてください。
「磁束密度Bの中を，長さlの導体棒が速さvで動くと，大きさV = Blv の誘導起電力が生じる。」
…さぁ，この文章のどこが変なのでしょう？
正解はこちら。
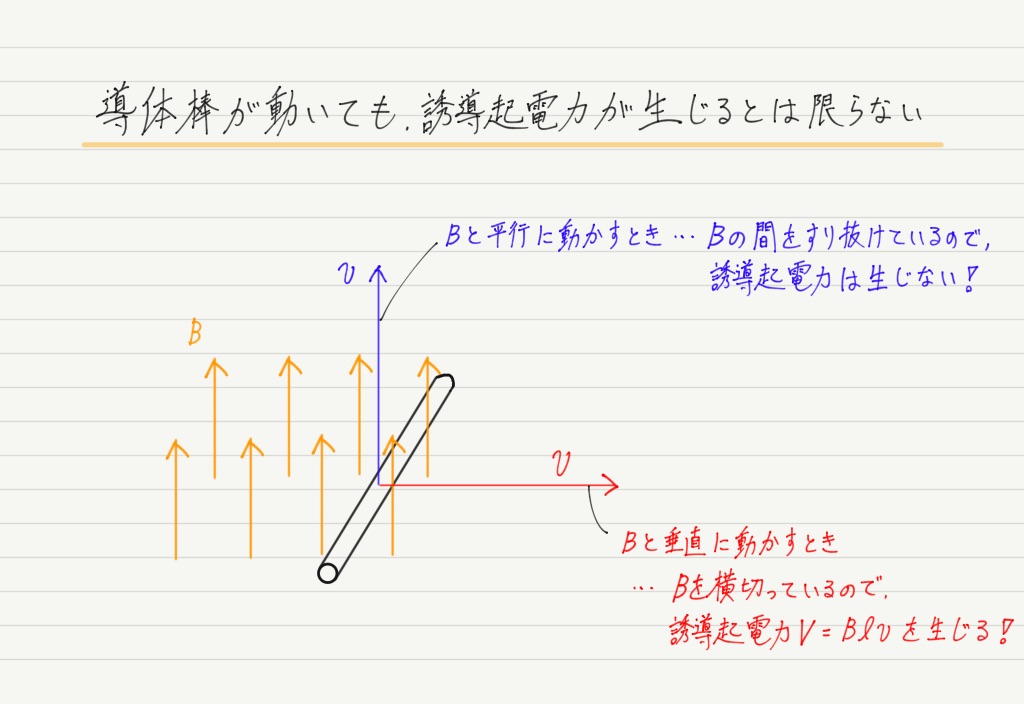
誘導起電力が発生するのは，導体棒が磁場を「動く」ときではなく，「横切る」ときです！
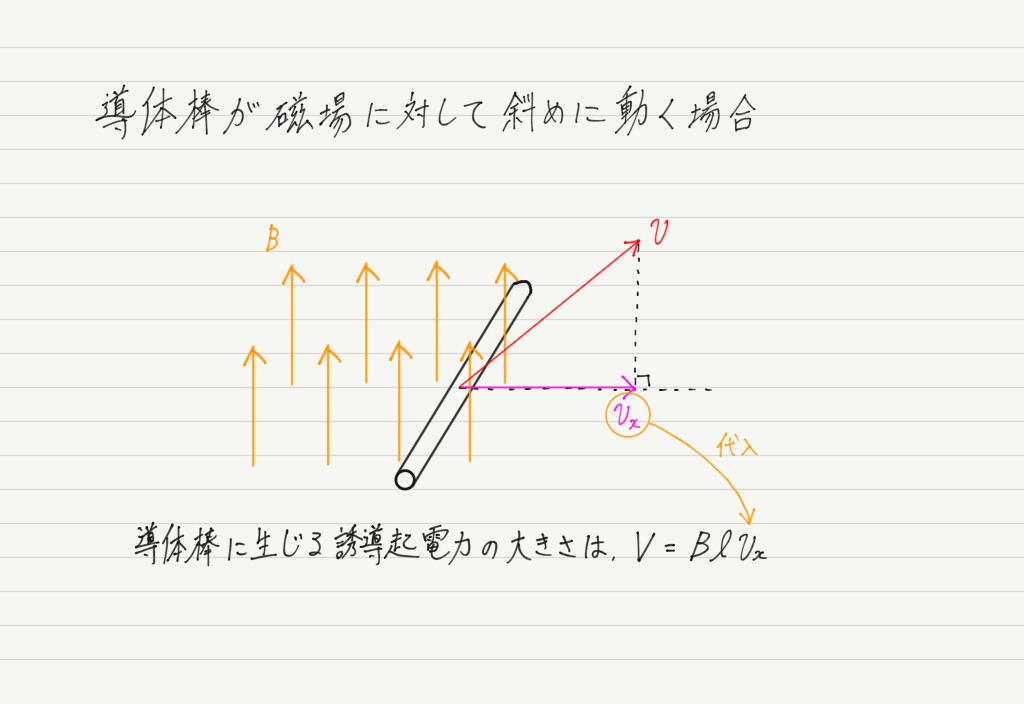
ちなみに，導体棒が磁場に対して斜めに動く場合は誘導起電力が生じます。
ただし，その場合は速さvをそのまま式に代入するのではなく，磁場に垂直な成分を使って計算してください。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
導体棒に誘導起電力が生じる理由を，ファラデーの電磁誘導の法則とは別のアプローチから考えてみたいと思います。
