前回は電磁誘導の頻出問題,「磁場を横切る導体棒」を扱いました。
導体棒に生じる誘導起電力の大きさと向きをファラデーの電磁誘導の法則とレンツの法則を駆使して求めましたが,今回は同じ問題を別の側面から見てみたいと思います。
タイトルにある通りローレンツ力に関する知識が必要なので,自信がない人はまずは復習してください。
誘導起電力はどこに発生する?
今回考えたいのは前回やった問題の(1)。(※(2)以降は誘導起電力とは無関係なので除外)
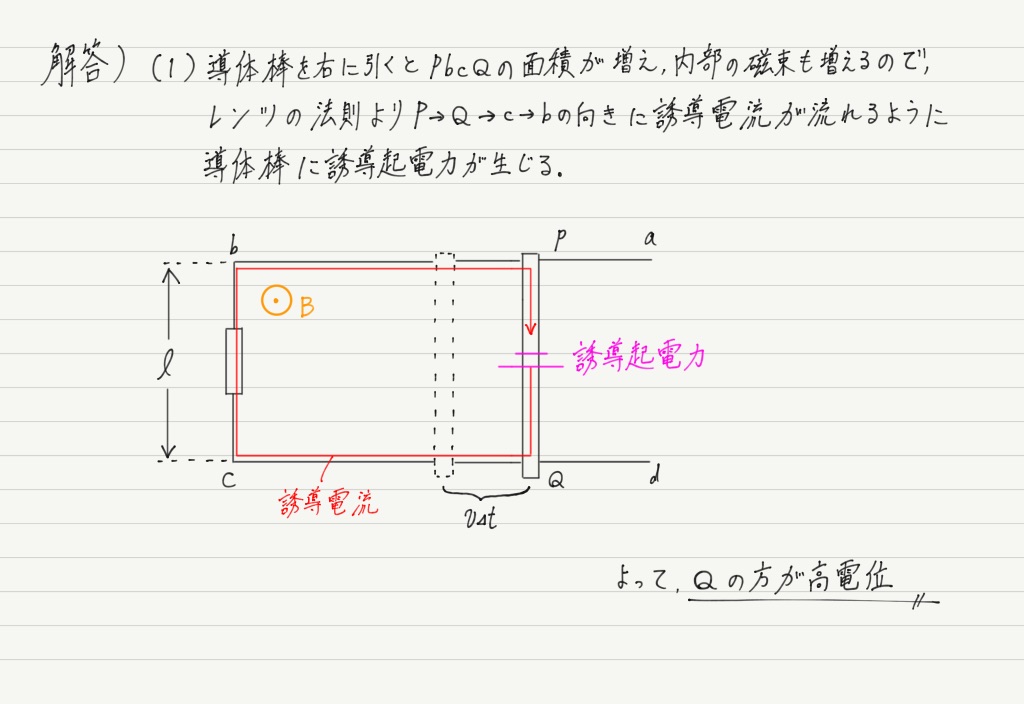
そしてこの問題に対する解答は以下の通りでした。
この解答,さらっと流してしまいそうですが,よく読むと疑問点も浮かびます。
もう一度冒頭から読み直してみましょう。
「導体棒を右に引くとPbcQの面積が増え」→ 当たり前
「内部の磁束も増えるので」→ そりゃそうだ
「レンツの法則よりPQcbの向きに誘導電流が流れるように」→ うんうん
「導体棒に誘導起電力が生じる」→ Why????
そう,この最後のところ!!
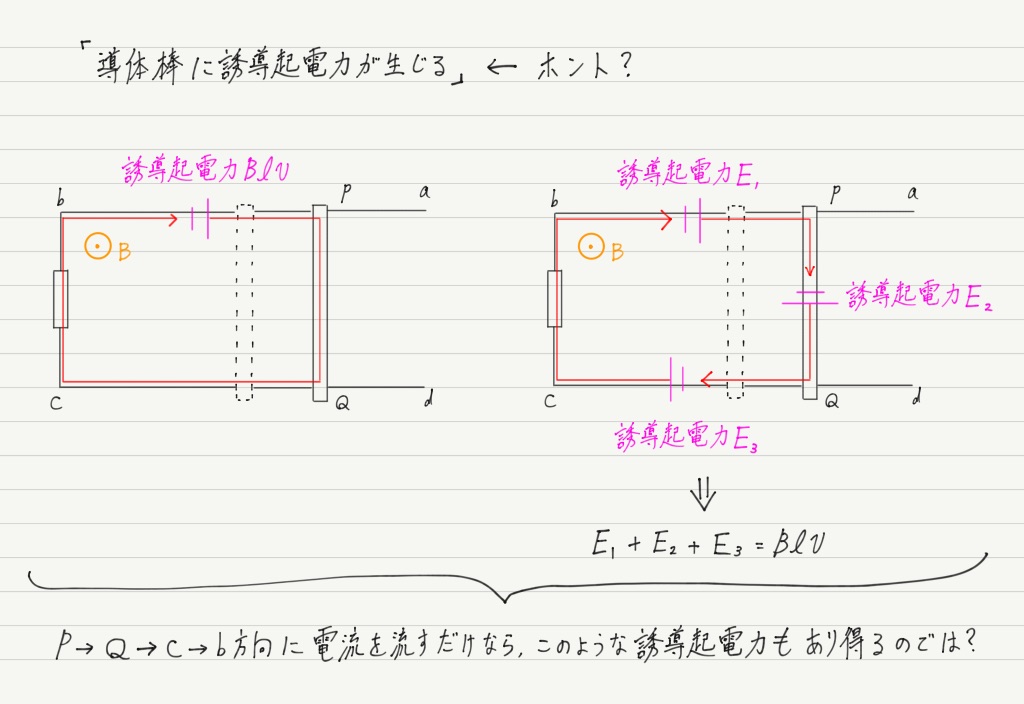
誘導起電力が生じるのはいいとして,なぜそれが導体棒に発生していると決めつけられるのでしょうか!?
回路の他の部分に発生しているという可能性は??
回路のいろんなところに複数発生しているという可能性は??
気になって夜も眠れませんね!笑
力学的なアプローチ
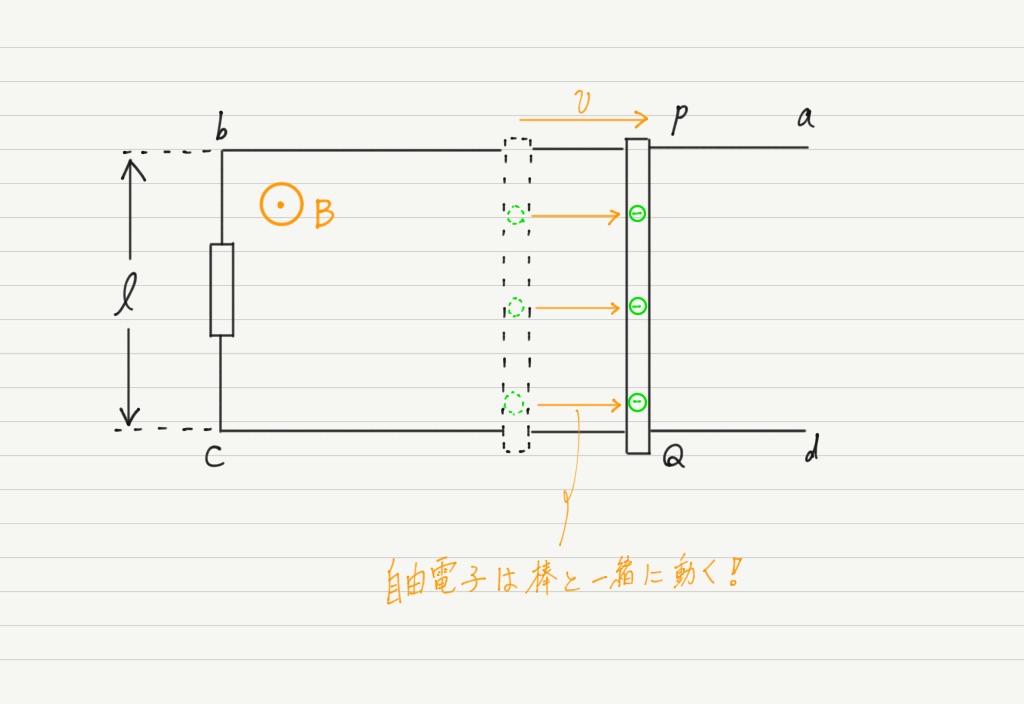
疑問を解決すべく,導体棒内部の自由電子に注目してみましょう。
導体棒を右に引っ張ると,導体棒の中の自由電子も一緒に右に動くことになります。
磁場の中を電子が移動したのだから,この自由電子たちはローレンツ力を受けることになります!
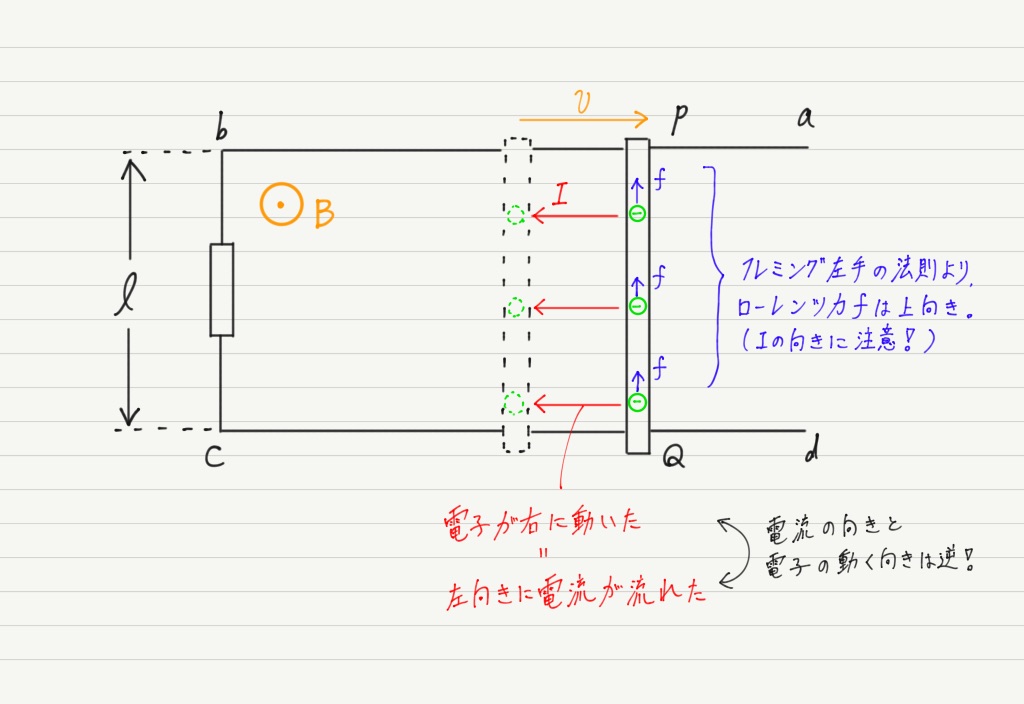
向きはフレミング左手の法則を使えばわかります。
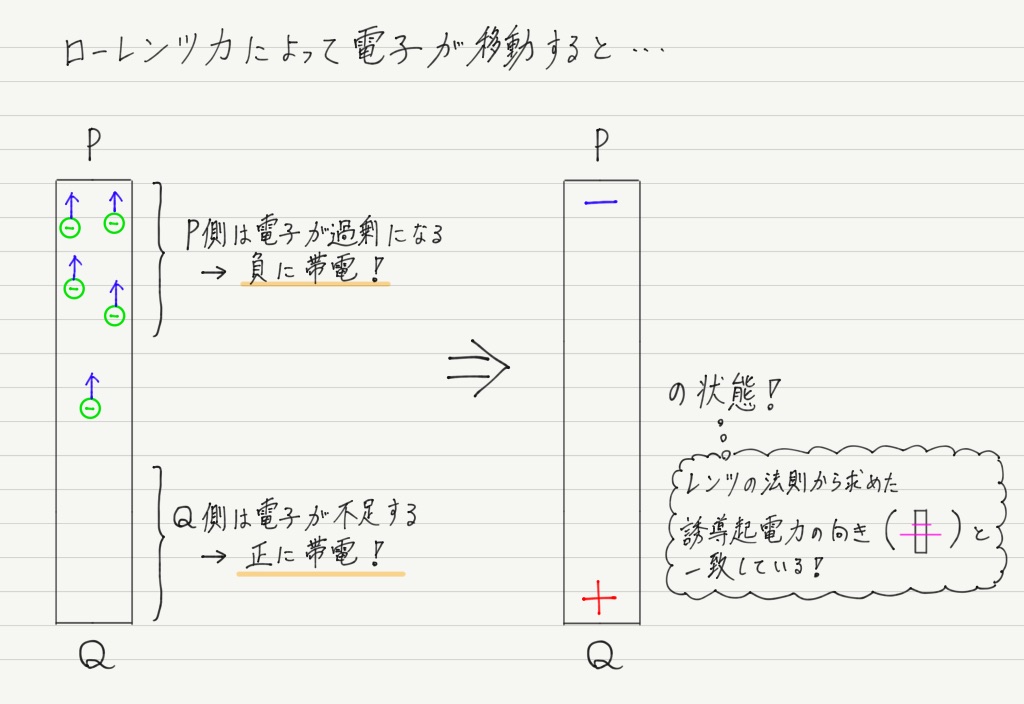
そしてローレンツ力を受けた自由電子はP側へ移動をはじめます。
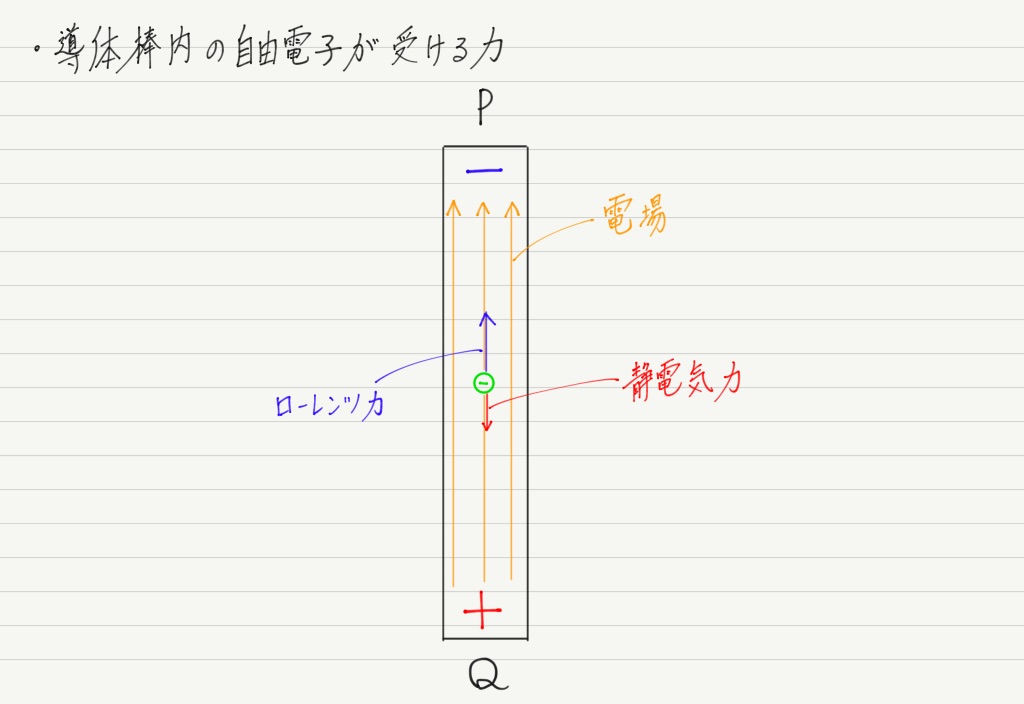
導体棒の両端が正と負に分かれると今度は電場が生じ,電子はローレンツ力の他に電場から静電気力を受けることになります。
はじめのうちは電場が弱いので,電子が受ける合力はローレンツ力の向きです(静電気力の大きさは電場の大きさに比例するから)。
よって,電場が形成されてもしばらくはP側への電子の移動は続きます。
しかし,電子の移動が進んで導体棒内部の正負の偏りが大きくなると,それに伴って電場も大きくなります。
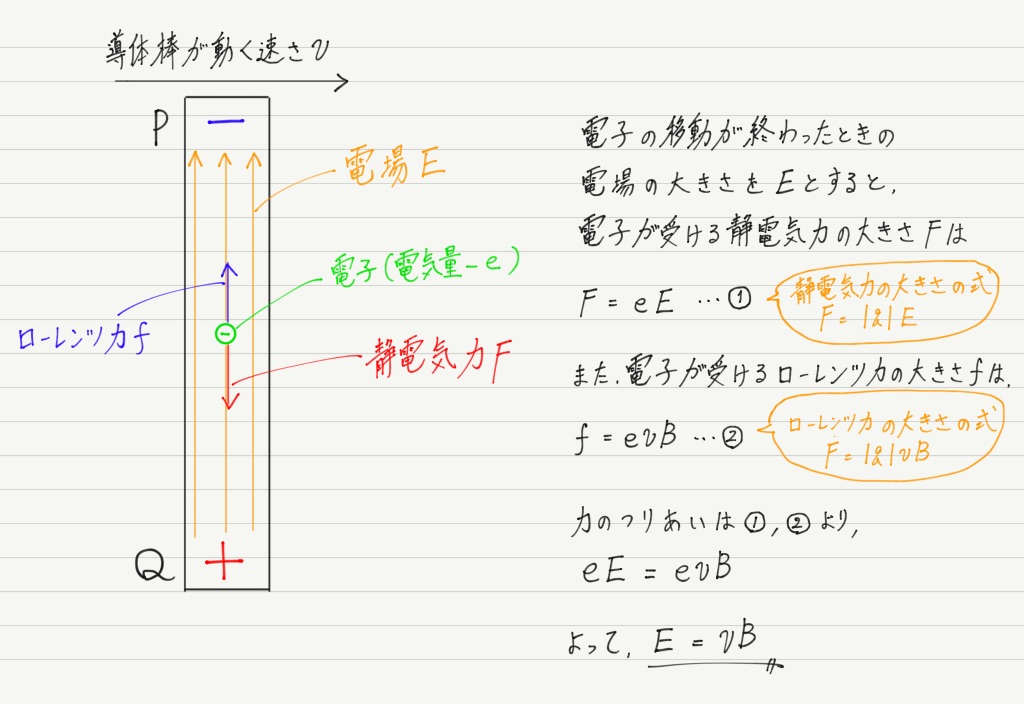
電場が大きくなれば電子が受ける静電気力も大きくなり,やがてローレンツ力とつりあいます。
そして最終的に力がつりあったところで電子の移動は終了。
では,移動が終了した時点での導体棒内部の電場の大きさEを求めてみましょう。
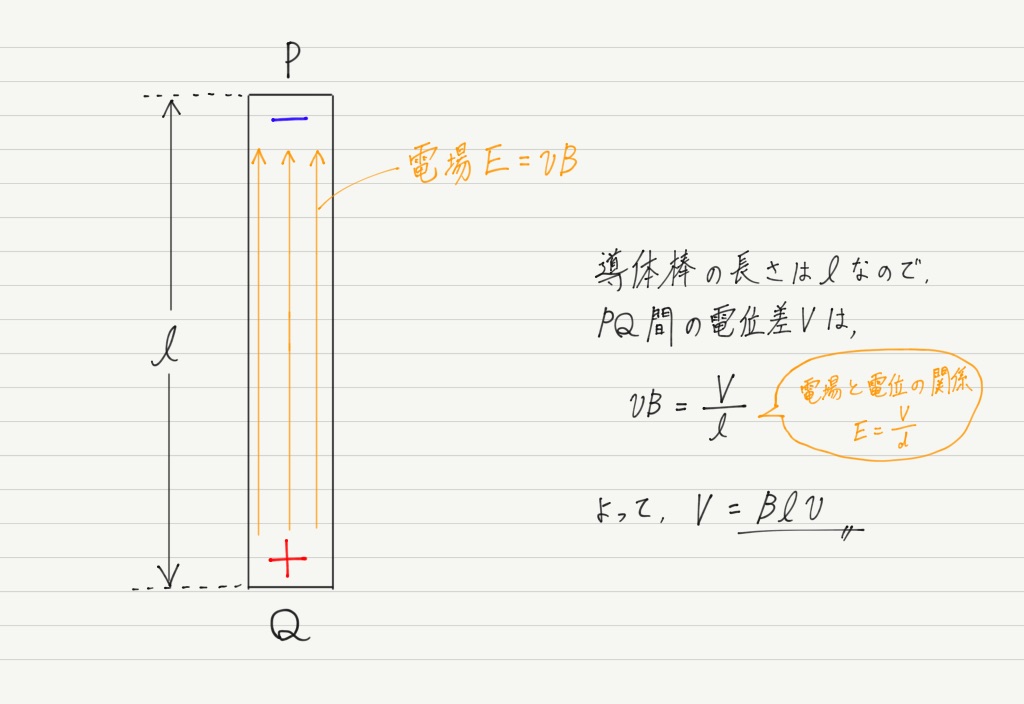
導体棒の長さを考えれば,PQ間の電位差も求めることができそうです!
こ,これは!
ファラデーの電磁誘導の法則で求めた誘導起電力の大きさと完全に一致してるではありませんか!!!!
これで冒頭の疑問は解決です。
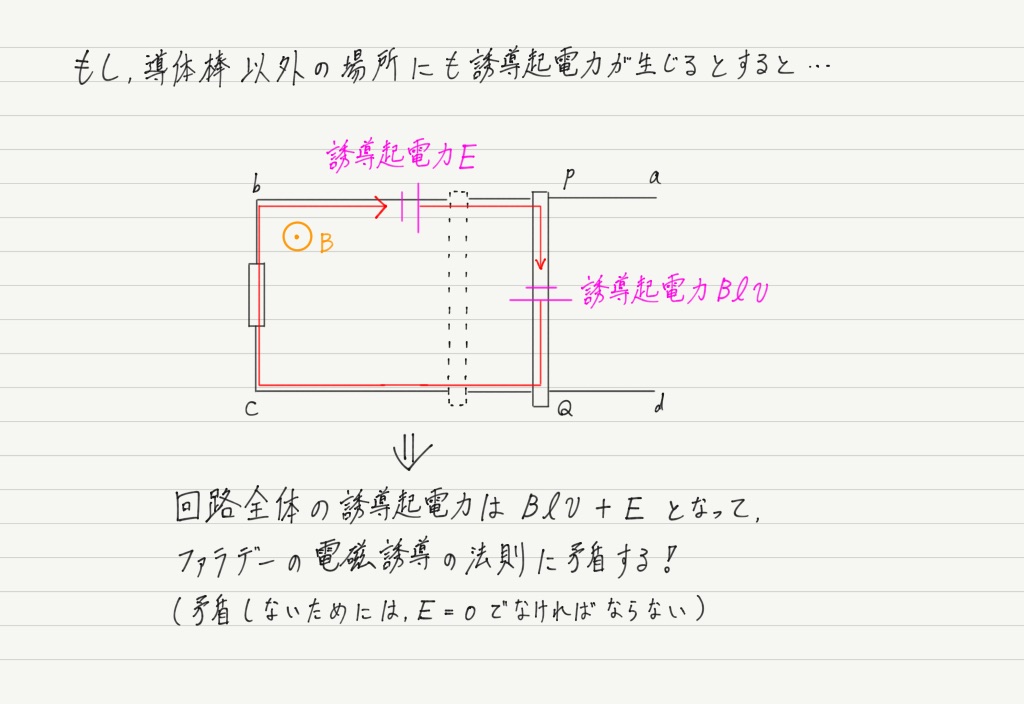
誘導起電力Blvは,導体棒(の中の電子の移動)だけで作り出されており,回路の他の部分に生じる余地はありません!
無事に「誘導起電力は導体棒にのみ発生する」ことが示されたので,これで安心して眠ることができます( ˘ω˘)スヤァ
今回は特に新しい話は出てきていない(ローレンツ力を復習しただけ!)ので,まとめノートはありません。
演習問題はあるので,時間に余裕がある人はぜひチャレンジしてみてください!
次回予告
回路(=1巻きコイル)の電磁誘導はこれにて終了。
次からはN回巻きコイルについての詳しい話に移っていきます。