ついに力学も最終講を迎えました!!
今回は万有引力を受けて運動する物体についての簡単な例題を解いてみたいと思います。
テーマは「宇宙速度」!
物体をすごい速さでぶん投げたら
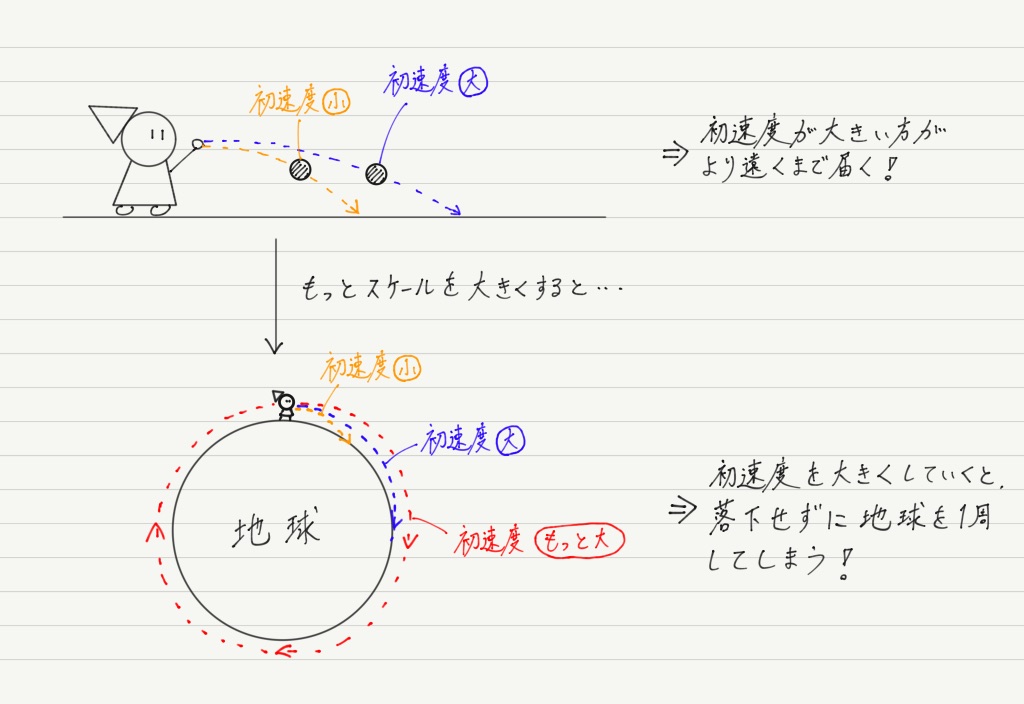
水平投射された物体はやがて地面に落下しますが,水平到達距離は初速度の大きさによって変化します。
速いスピードで投げればそれだけ遠くまで届く。
ここまでは当たり前の話ですが,この話を極端に考えてみてください。
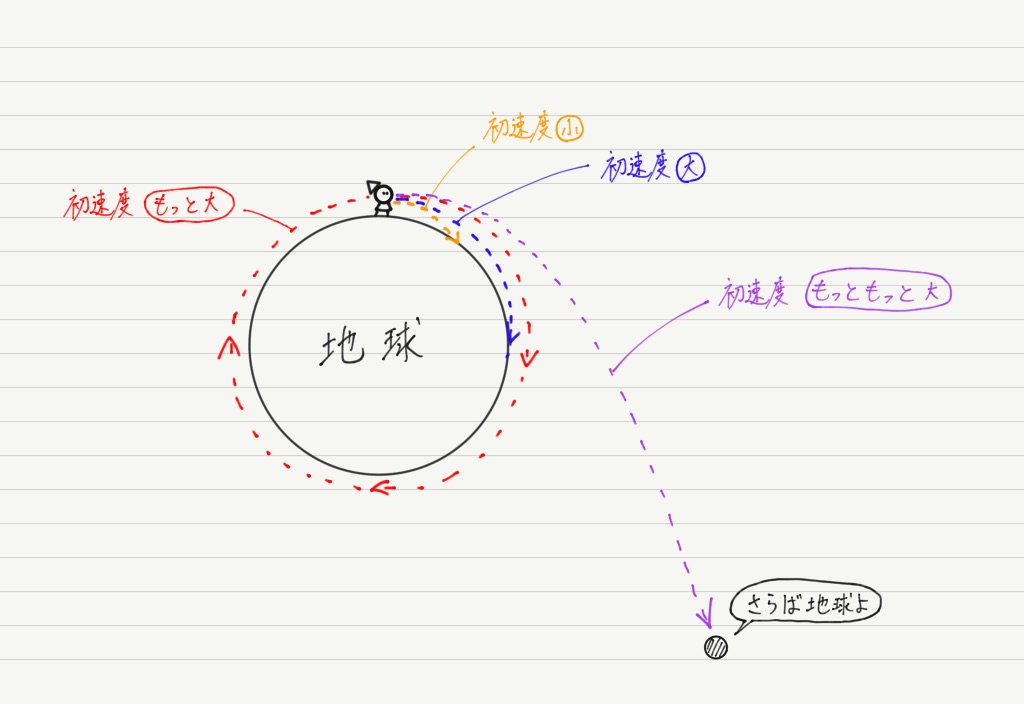
どんどん初速度を上げていったら,そのうち地球1周することになりますよね!
さらにそれ以上の初速度で投げたら,もう重力を振り切って地球から離れていってしまいます。
このように物体が地球を周回したり,地球から離れていってしまうための初速度はいくらなのか,具体的に求めてみようというのが今回の課題です!
例題
実はこれ,ここまで習った知識で求められちゃいます。
例題という形でやってみましょう。
解答・解説はこの下にあるので,解けたら(もしくはまったくわからなかったら)先に進んでください。
解答はこちら ↓
今回の問題は,Rとgだけを用いて答えなければいけないことに注意してください(この手の問題は割と多い)。
答えに万有引力定数Gを使ってはいけない場合は,gとGの関係式を使ってGを消去するのが鉄則!
(gとGの関係式は万有引力の記事に登場しているので忘れている人は復習すること。)
続いて(2)の解答もどうぞ。
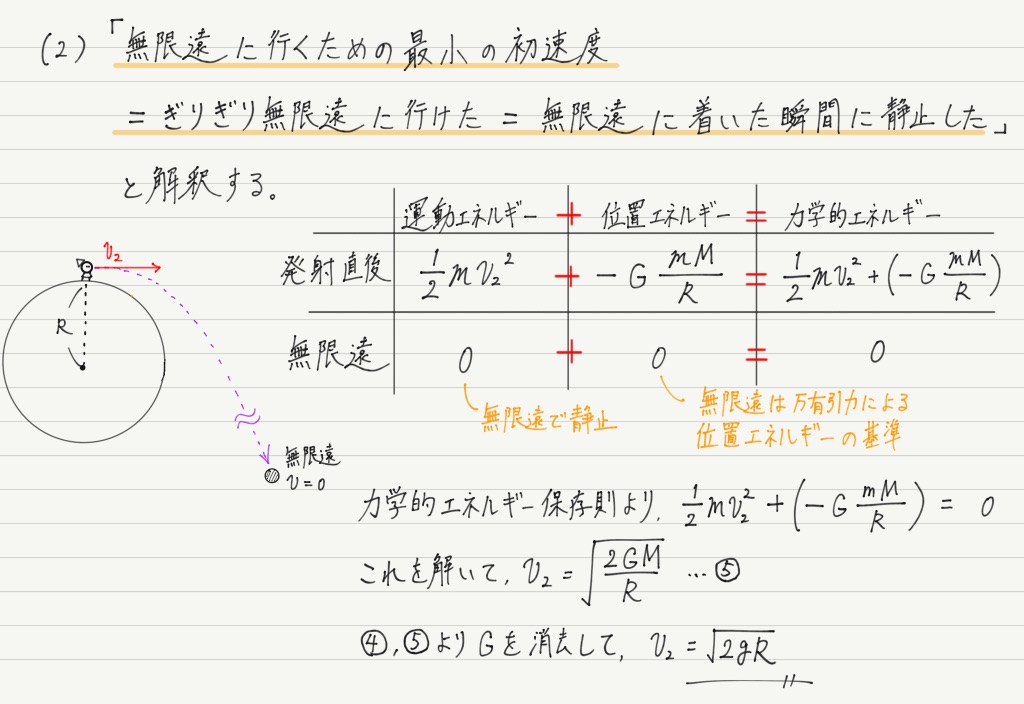
(2)は初見ノーヒントで解くのは正直難しいと思います。
「無限遠に行くための最小の初速度」を「無限遠で速度0になるときの初速度」と読み換えて,エネルギー保存則に持ち込んでください。
ただし初見では難しくても一度でも解いたことがあれば言い訳は通用しませんので,これを機にこの求め方を身につけておくこと。
ところで,いま求めた第1宇宙速度と第2宇宙速度の式をよーく見比べてみると…
地球の周りを回り続けるための速さと,無限の彼方へ飛び去るための速さが約1.4倍しか違わないって驚きじゃないですか?
人工衛生を打ち上げるとき,本当は周回させようとしたのに,ちょっと設定をミスって少し速度が出すぎてしまったらもう2度と地球に戻ってこれないということです。
もし人が乗っていたら? 怖っ!
今回は特に新しい内容を勉強したわけではなく,「万有引力を受ける物体の運動は,円運動で習った知識やエネルギー保存則を使えば調べられる」というのが結論なので,まとめノートはありません。
演習問題を用意したので,時間がある人はぜひチャレンジしてみてください! より一層理解が深まります。
さて,物理基礎の力学から数えて全55講(補講を除く)。
高校物理最大のボリュームを誇る力学でしたが,ついに完結。
力学は物理の学習のすべての基礎なので,ここからステップアップされる方も,他の分野の学習に進まれる方も,何かにつまずいたらここに復習しに戻ってきてください。
ここまで読んでくださった皆様,本当にありがとうございました。