交流電圧をかけたコイルが,どのような特徴を示すのかを見ていきましょう!
コイルと位相のずれ
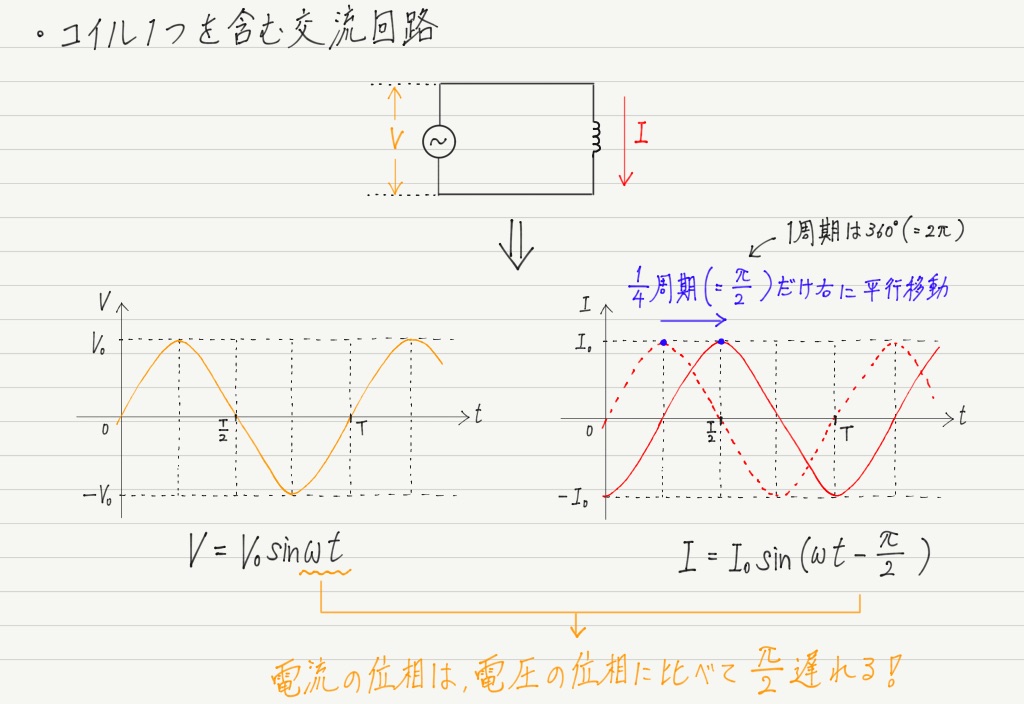
抵抗の場合には電圧と電流の位相はずれないという拍子抜けな結果でしたが,コイルの場合,電流の位相は電圧よりも遅れます。
これはしっかり覚えておいてください!
(「位相が遅れる」って何?という人は前回の記事で復習しましょう!)
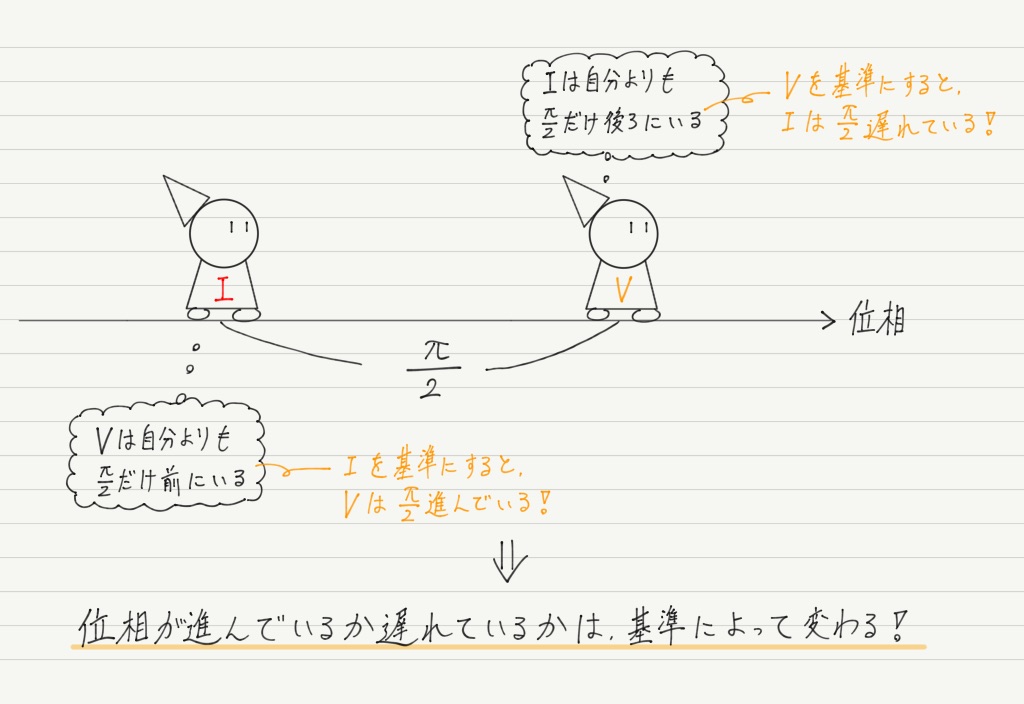
おっと,ここでひとつ注意点。
上の図では電圧の位相を基準にしていますが,逆に電流の位相を基準にして「電圧の位相は電流より進む」と表現する場合もあります。
なので単純に「コイルの場合は位相が遅れる」なんて覚えちゃダメ。
ちゃんと基準も含めて覚えるようにしてください!
電流と電圧の関係
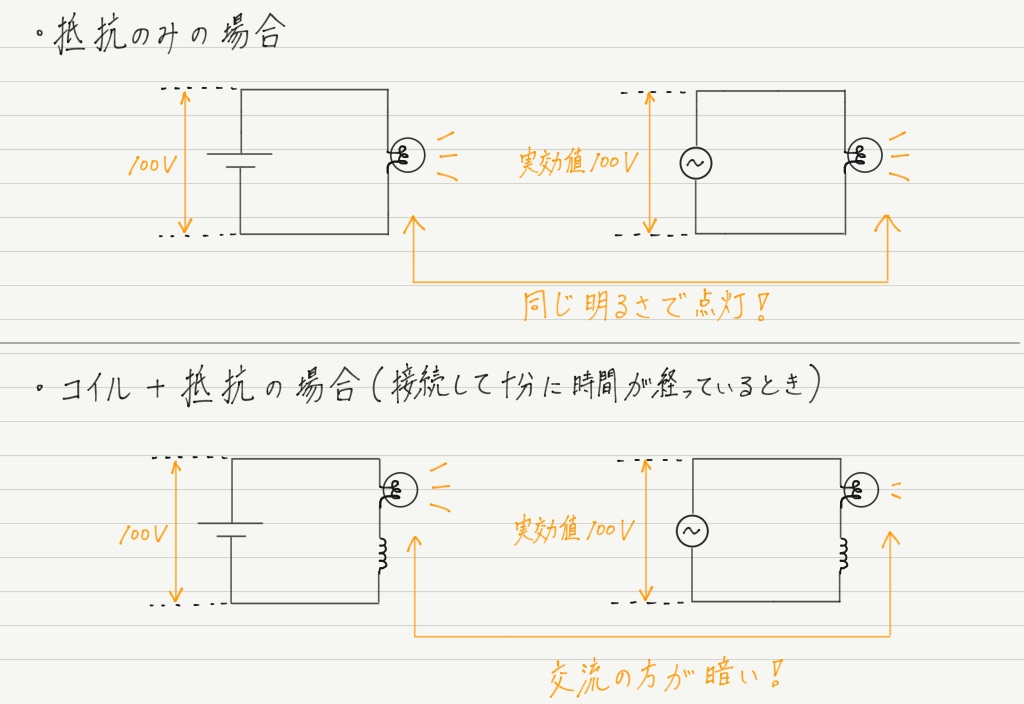
実効値の話を思い出してください。
抵抗に直流電圧を加えたときと,同じ実効値の交流電圧を加えたときでは流れる電流は等しくなります。
ところが,抵抗とコイルを直列接続した場合,流れる電流は交流のほうが小さくなります!
交流だと電流が流れにくくなるということは,コイルは交流に対して “抵抗と同じはたらき” をしていると考えられます。
ただし同じはたらきとはいえ,抵抗とはもちろん別物。
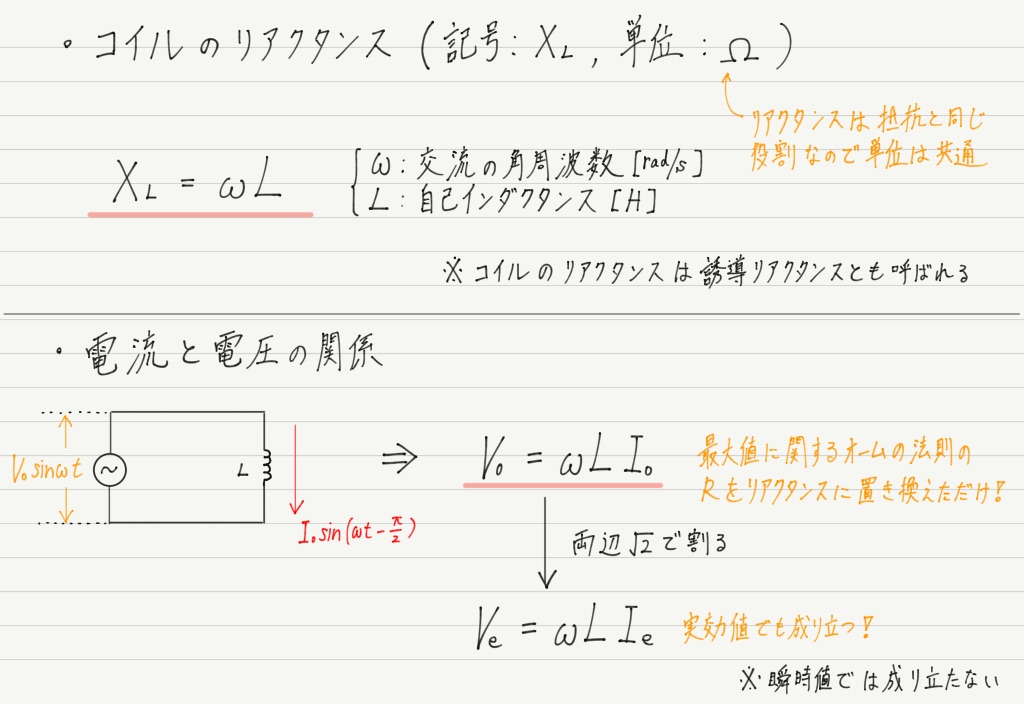
区別するために,コイルがもつ抵抗のはたらきのことをリアクタンスと呼ぶことにしましょう。
リアクタンスを用いると,コイルに加わる電圧の最大値とコイルを流れる電流の最大値に関して,オームの法則と同様の関係式が成り立ちます!
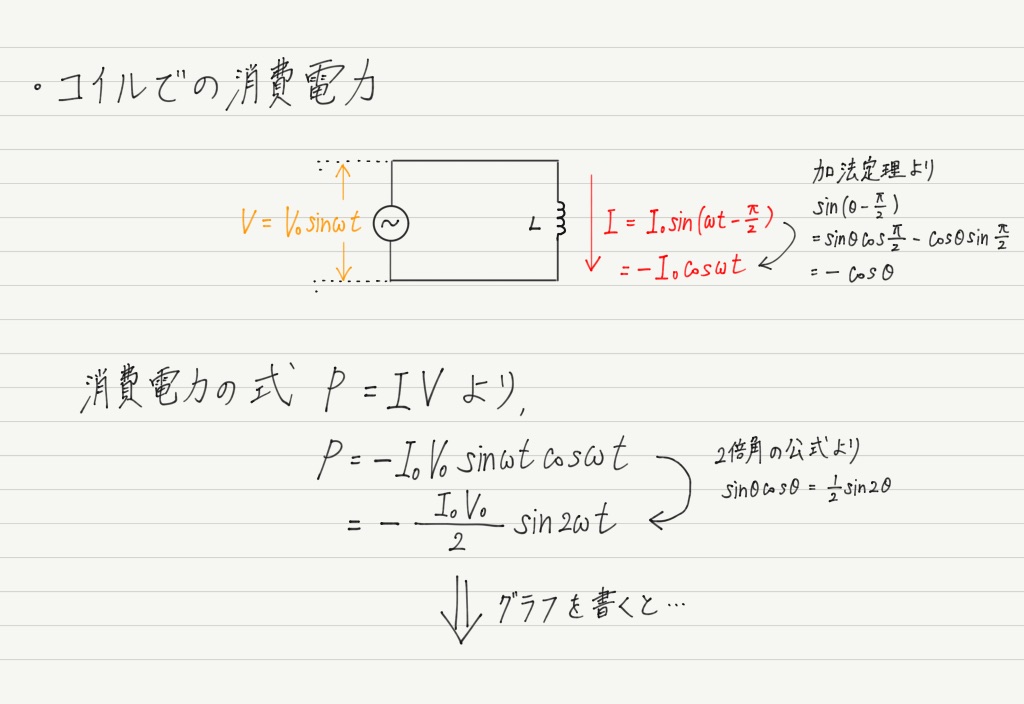
消費電力の平均
抵抗とリアクタンスは単位も同じ,最大値や実効値についてオームの法則が成り立つところも同じですが,最大のちがいは消費電力。
説明するよりも実際に計算したほうが早いので早速やってみましょう。
抵抗のときもそうでしたが,交流の場合は消費電力の平均が大事なので,平均を求めてみたいと思います。
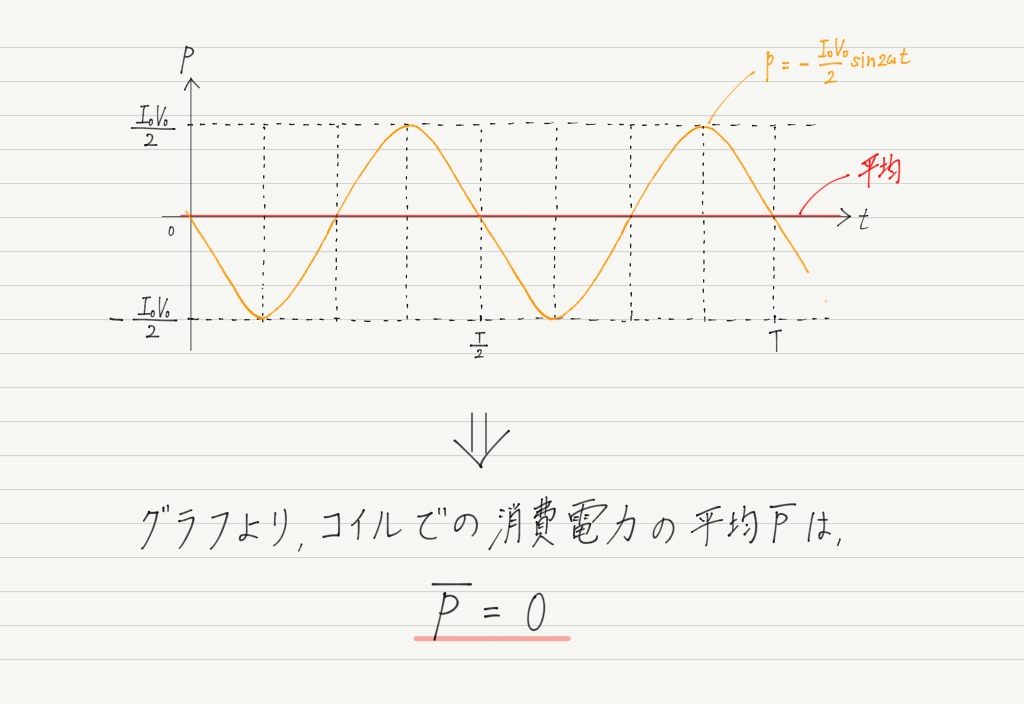
このように,コイルの消費電力の平均は0になってしまいます! これは面白い結果!
(※ あくまで「消費電力の平均が0」なのであって,「消費電力が常に0」ではないことに注意。グラフからわかるように,各時刻では消費電力は正の値と負の値を周期的に繰り返している。)
抵抗がジュール熱としてエネルギーを消費するのに対し,コイルは平均するとエネルギーを消費しないということです。
短いですが今回はこれで終了。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください!(今回のまとめノートはなし。次回のまとめノートに今回の内容も含めて書きます。)
次回予告
次回は「コンデンサー1個だけ回路」を扱います!