高校物理の力学の花形である単振動。
本編ではそのオーソドックスな例として,水平ばね振り子と単振り子を扱いました。
…あれ? ばねって別に水平にしなくても振動するじゃん??
ってことで,さっそく例題を使って解説したいと思います!
例題
今回はばねを天井から吊るして振動させる,いわゆる鉛直ばね振り子の問題です。
この問題を題材に解説していきますが,力学に自信のある人は解説を読む前に自力で解いてみてください。
ちょっとこれは無理かな…という人はすぐ解説に進んで構いません。
解答・解説
では早速(1)と(2)の解答から見ていきましょう。
ばねを水平から鉛直にしたことで生じる最大の変化は,運動方程式に重力mgが登場することです。
そして,それによってある重大な問題が生まれます。 それは…
運動方程式に重力が加わったことで,単振動の運動方程式の形になっていない…
ということは鉛直ばね振り子は単振動じゃない…?
ざわ…ざわ…
いえ,ご安心を。 鉛直ばね振り子も間違いなく単振動します。
じゃあ,運動方程式の形がちがうという問題はどうするかって?
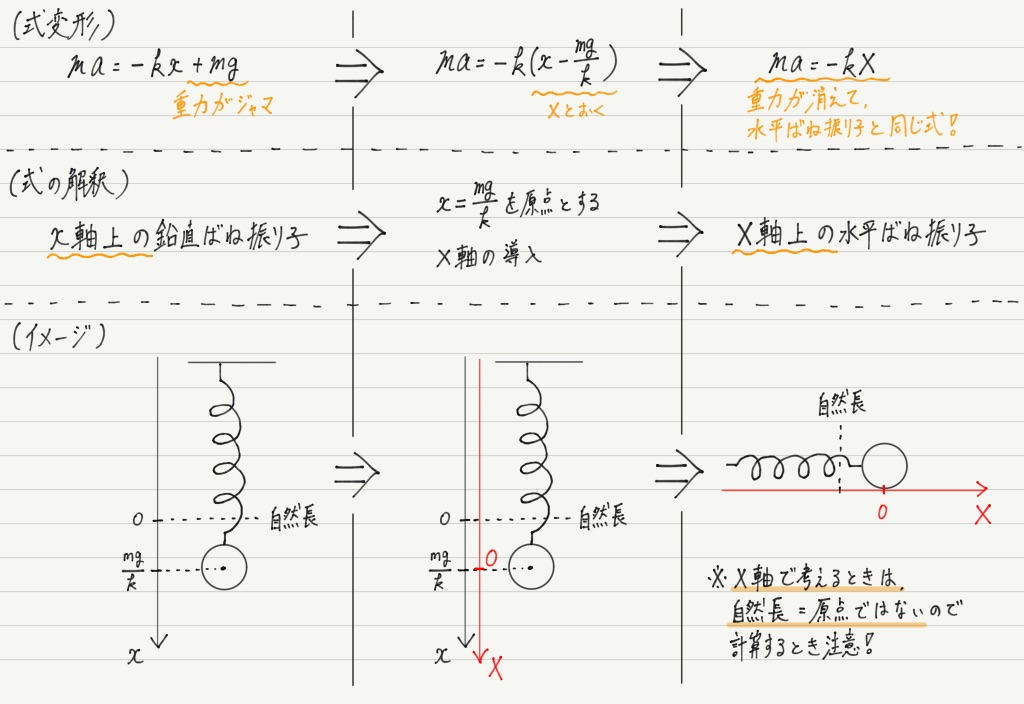
まぁ,見ててください。 ちょいと式変形を施します。
ほら!単振動になった!! やったね!
…え? その式変形,強引すぎないかって?
確かにこれだけ見ると,結論ありきで無理やり式変形しているように見えるかもしれません。
が,そんなこと言わずに,この式変形をもう少し掘り下げてみましょう。
これはすごい!!
結局,さっきの一見強引な式変形は,「軸をうまく取り直すと,重力の影響を消せる(=水平ばね振り子の問題として考えられる!)」ということを示していたわけです!
いやぁ,式変形もやってみるもんですねぇ。 そうなると,(3)も楽勝。
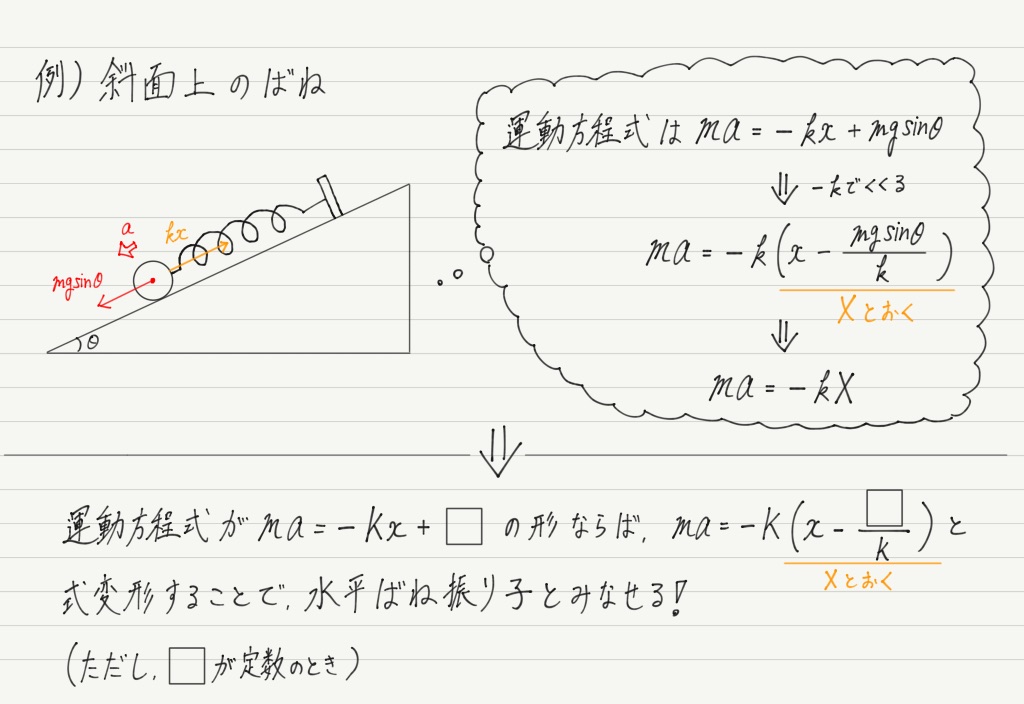
このように,鉛直ばね振り子の問題は「式変形して水平ばね振り子の問題に持ち込む」だけであっさり解くことができます!
ちなみにこのテクニックは鉛直じゃなくても使えます。
ぜひマスターしましょう!
(おまけ)まともに解こうとすると…
この式変形を知らない人(またはそういうテクニックを嫌う人)がこの問題を解こうとするとどうなるかお見せしたいと思います。
式変形を知らなくても(1)や(2)は問題ないし,(3)の周期も公式そのままなので大丈夫でしょう。
でも,一番差が出るのは力学的エネルギー保存則を使うときです。 さっきの解答と比較してみてください。
重力による位置エネルギーまで出てくると,単純にその分だけ計算が長くなってしまいます。
この例題は簡単なので,これぐらいで済んでいますが…
長い式でも正しく計算すれば正しい答えが出るけど,同じ答えが出るならそりゃ簡単なほうがいいですよね〜
今回やった式変形は受験のためのテクニックなどではなく,運動の本質(水平だろうが鉛直だろうが,結局は同じ単振動!)を見極めるためのもの。
「見方を変えるとこんなにスッキリするんだ!」ということを実感して,今後の物理の勉強に活かしてください!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。