物理基礎【電磁気】補講『自由電子の運動と電気現象』の講義内容に関連する演習問題です。
講義編を未読の方は問題を解く前にご一読ください。
問題
長さL,断面積Sの円柱状の導体がある。
この導体の両端に電位差Vを加えると,自由電子(質量m,電気量−e)は電場から力を受け加速される。
導体内の自由電子の数は単位体積あたりn個として,以下の各問に答えよ。
[Level.1]
自由電子の平均移動速度をvとする。
導体を流れる電流の大きさIを,L,S,V,m,e,n,vのうち必要な記号を用いて表わせ。
[Level.2]
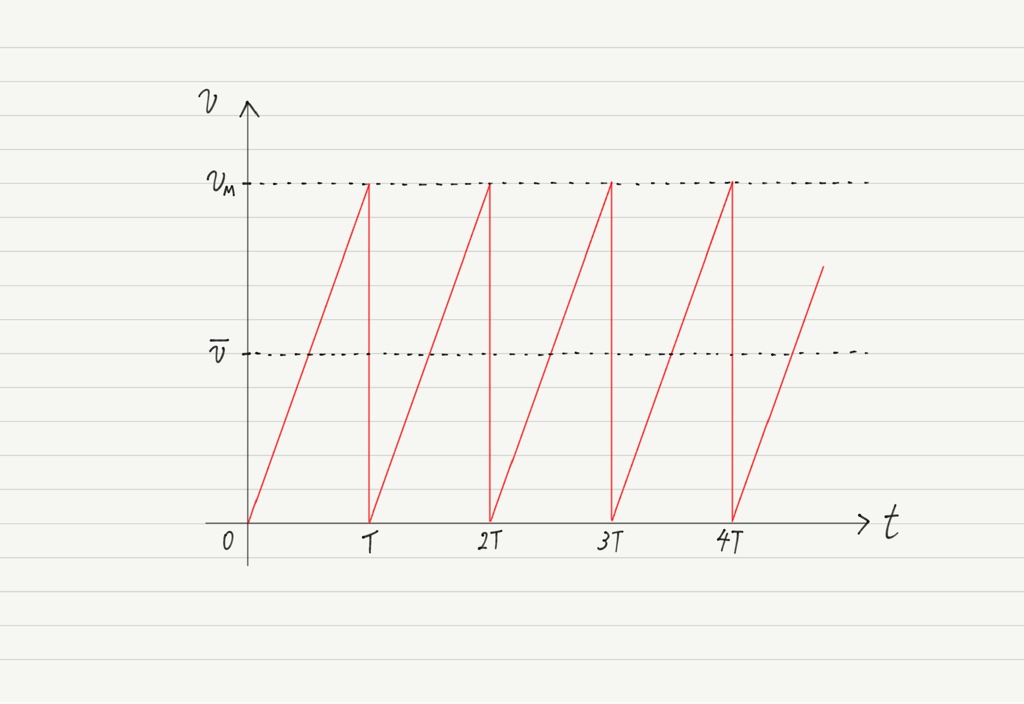
導体内の自由電子は以下のv-tグラフに示すように,一定時間Tごとに原子に衝突して速度が0になると仮定する。
図中のvMを,L,S,V,m,e,n,Tのうち,必要な記号を用いて表わせ。
[Level.3]
v-tグラフより,vはvMの半分であることがわかる。
このことと前問までの結果を利用して,この導体の抵抗率ρを,L,S,V,m,e,n,Tのうち必要な記号を用いて表わせ。
この下に答えを載せていますが,まずは自力で考えてみましょう。
答え
[Level.1]
I=enSv
[Level.2]
\(v_{M}=\frac{eVT}{mL}\)
[Level.3]
\(\rho =\frac{2m}{e^{2}nT}\)