いよいよ抵抗,コイル,コンデンサーの3種類すべてが接続された回路に挑戦しましょう!
今回は手始めに直列接続の場合について見ていきたいと思います。
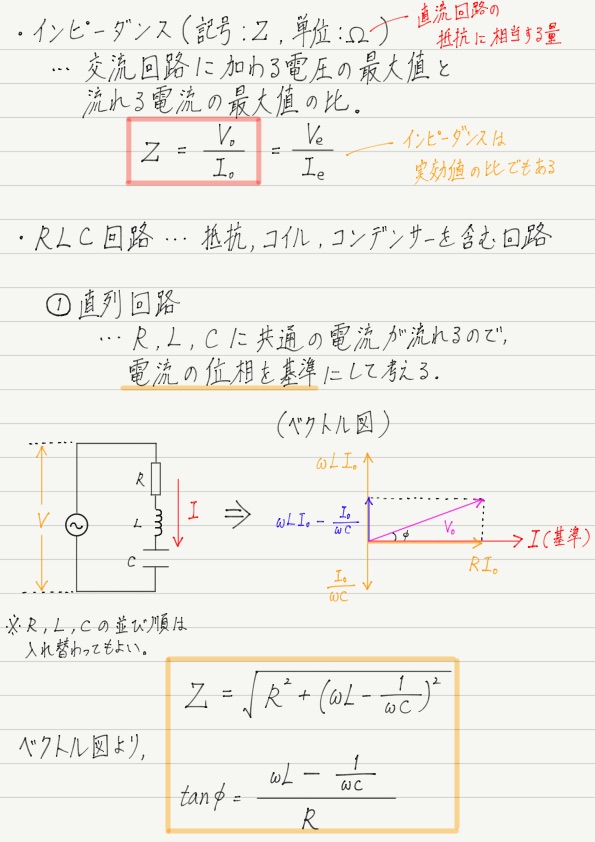
ベクトル図を用いたインピーダンスの求め方
RLC直列回路のインピーダンスと位相のずれを求めるのが今回の最終目標です。
…と,その前に。
前回の講義で三角関数の合成を用いてRL回路のインピーダンスを計算しましたが,ちょっとめんどくさかったですよね?
RLC直列回路の説明に先立って,まずはインピーダンスを簡単に求める “裏技” を伝授しましょう!
前回やったRL直列回路の例題を使いまわして解説します。
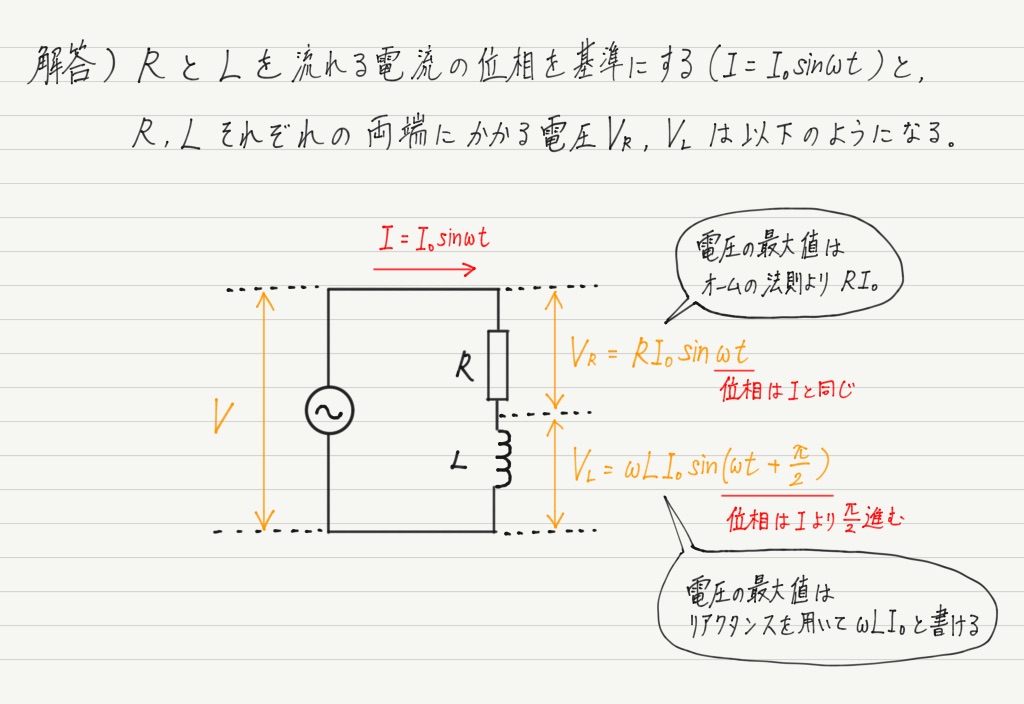
さっそく解いていきますが,電流の位相を基準にして抵抗,コイル両端の電圧を書き出すところまでは前回やったのと同じ。
ここからいよいよ裏技,その名も「ベクトル図」に突入します!
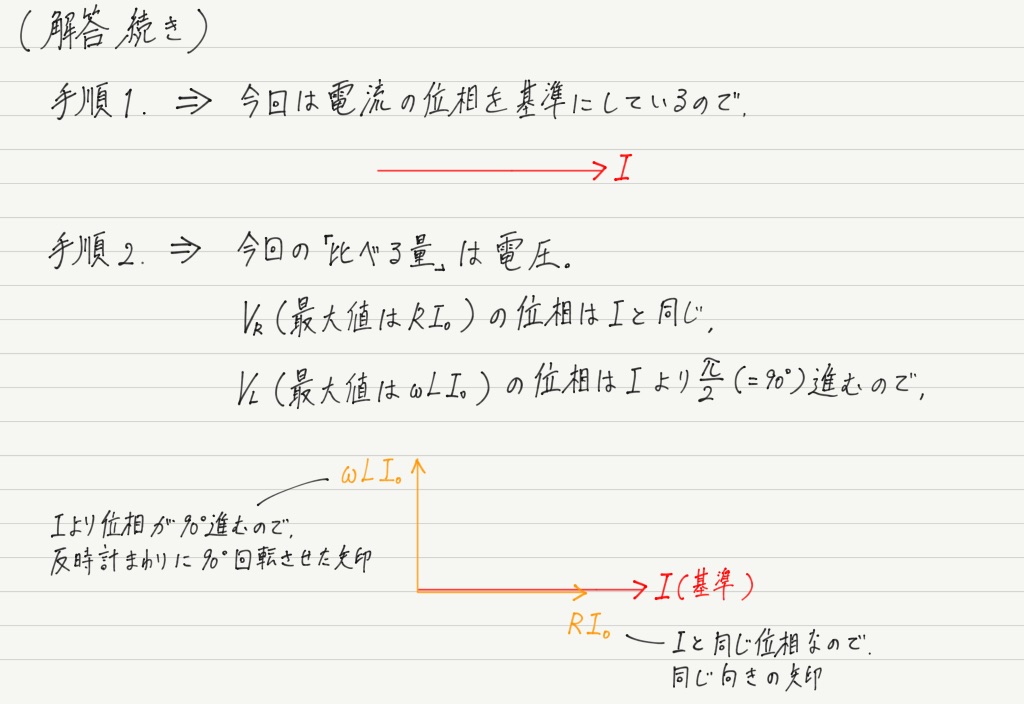
まずはその手順を紹介。
手順だけ見せられてもわかんないと思うので,例題の続きをこの手順に沿って解いていきましょう!
ほら,前回と同じ答えが得られました! 三角関数を合成するより簡単じゃない? これぞ裏技・ベクトル図の威力!
※ 注意!!
電磁気の勉強をしっかりやってきた人はこのやり方に違和感を感じていると思います。
どこかわかりますか?
「電圧を矢印で表してるけど,電圧ってベクトルじゃないでしょ!」っていうツッコミができれば合格。
そう,電圧(=電位差)って向きをもたないスカラー量でしたよね?
にも関わらず,上のやり方では電圧を矢印を使って表し,しかもベクトルの和まで計算しています。
私がベクトル図を “裏技” と呼ぶ背景には,「本当はベクトルじゃないのに,ベクトルだと思って計算するとなぜか正しい答えが出る」という想いが込められています。
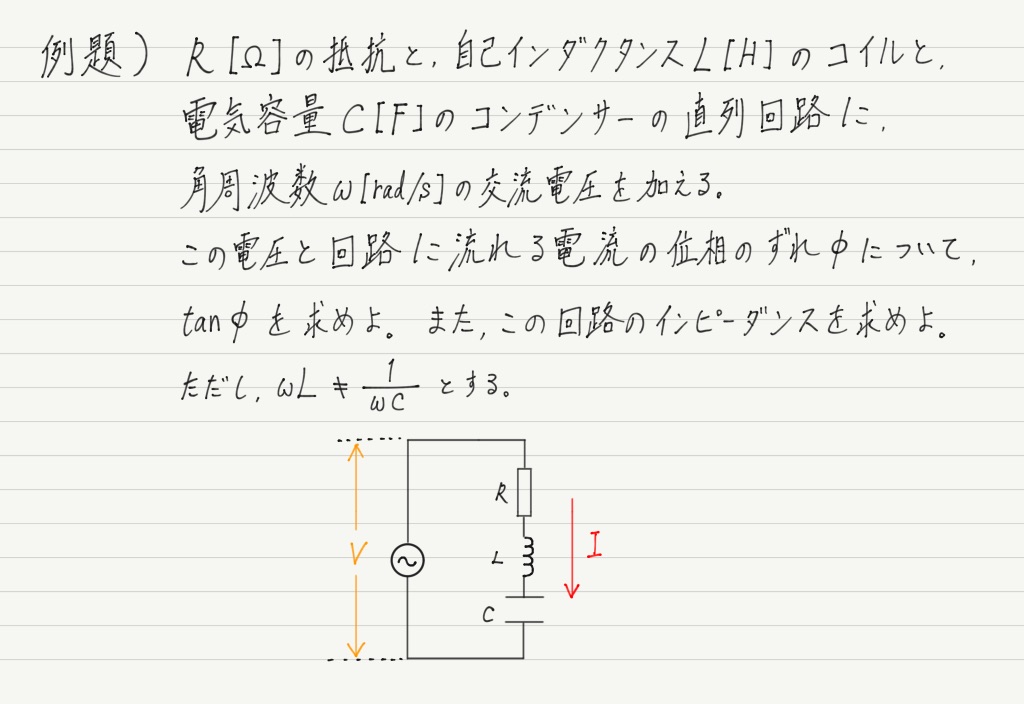
RLC直列回路のベクトル図
では,いよいよ本題に入ります。
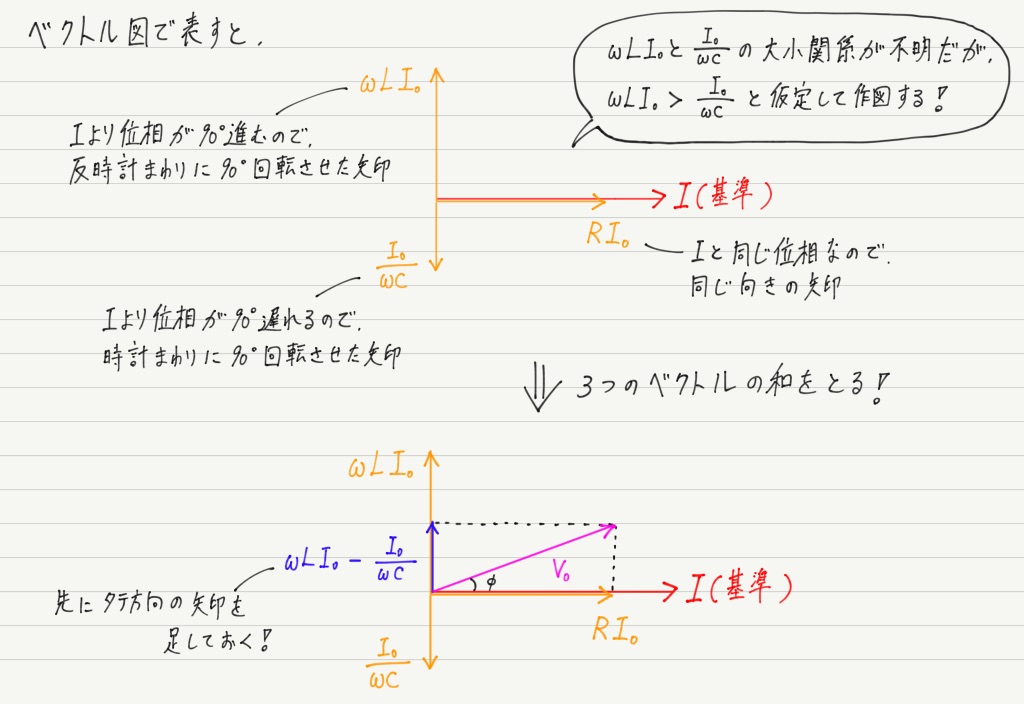
ベクトル図を使って解いてみましょう! まずは位相のチェックから。
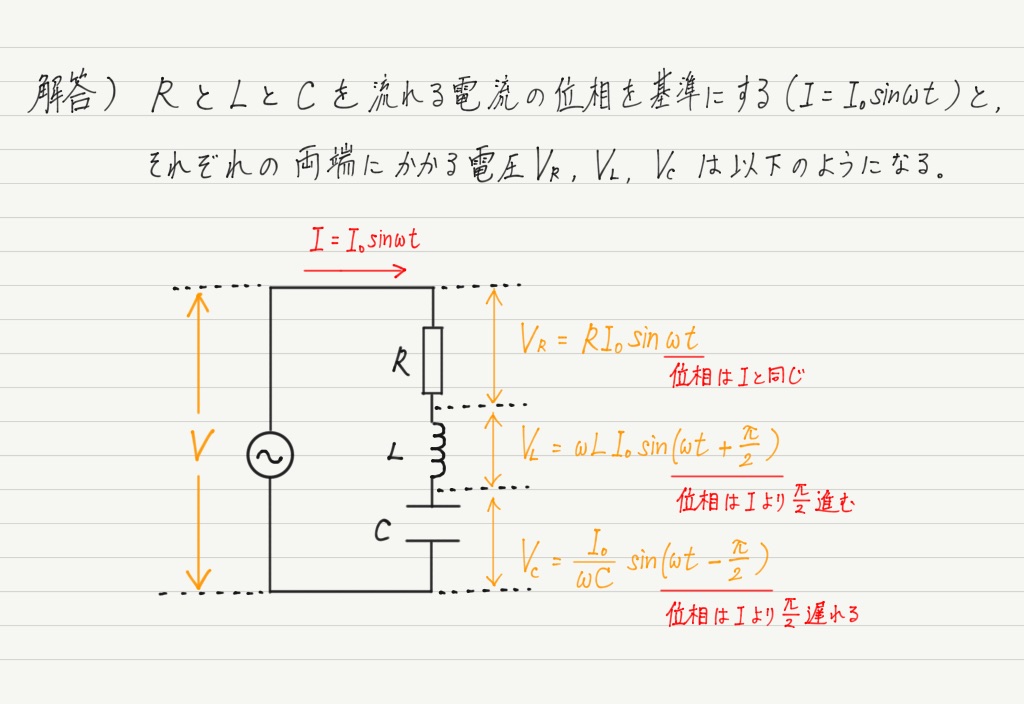
直列なのでさっきと同様に電流の位相を基準にします。
これをもとにベクトル図を書きます。 今度はRLCなので矢印3本ですよ!
はい,これでおしまい。
RLC回路と聞くと難しそうに思えますが,ベクトル図にかかればこの通り。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
直列回路はこれでバッチリ。 こうなると,並列回路がどうなるかも気になるところですよね!