電気回路で抵抗を扱うための法則といえば,もちろんオームの法則!
…なのですが,オームの法則が成り立たない抵抗というものも存在します。
今回はそんなおかしな抵抗の振る舞いについて学んでいきましょう。
抵抗と温度
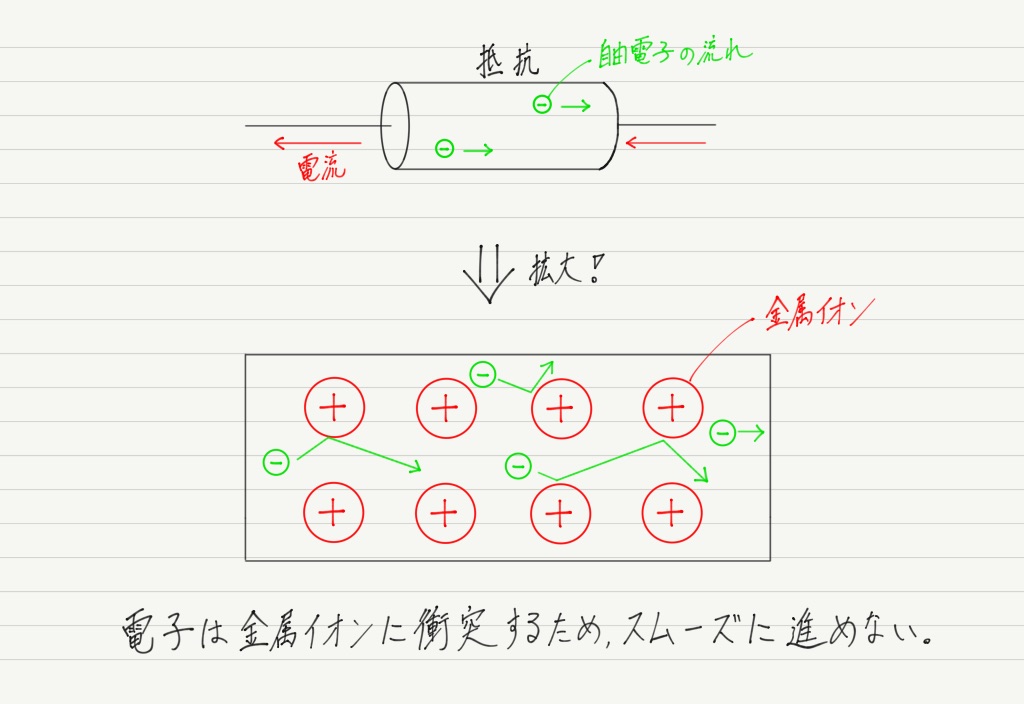
抵抗というのは電流(自由電子)の流れにくさですが,そもそもなんで流れにくいのでしょうか?
実は,金属の陽イオンが流れにくさを生み出している原因です。
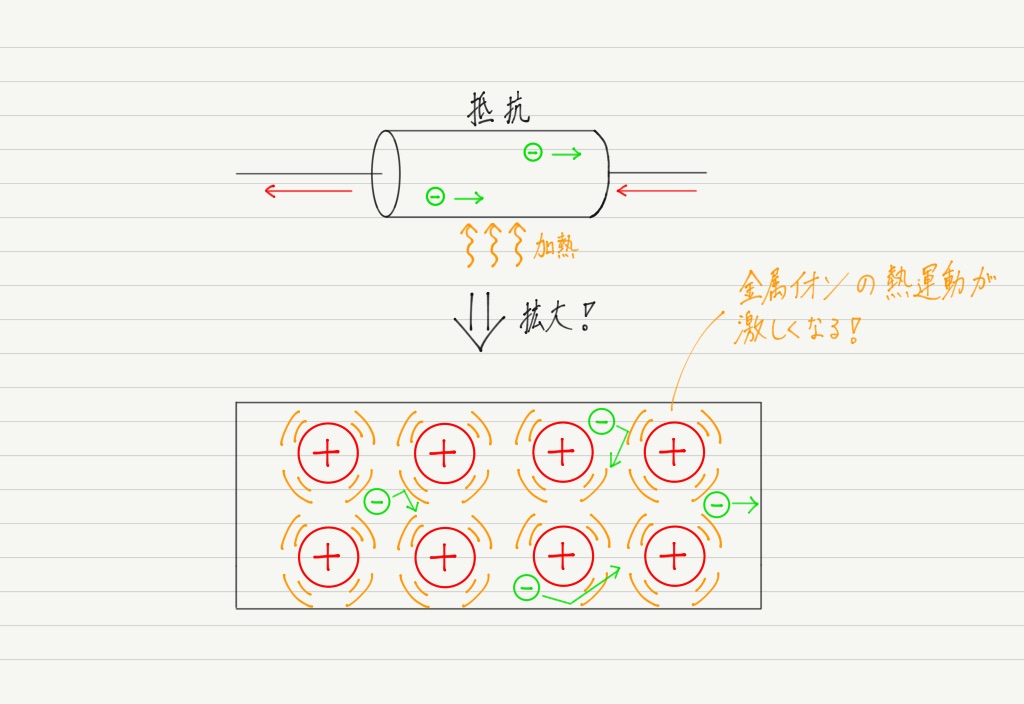
突然ですが,ここで金属の温度を上げてみましょう!
金属イオンの熱運動が激しくなると,自由電子の通りにくさは加熱前よりも増します(=抵抗値の増加)。
サッカーやバスケでも,動きの遅いディフェンスを抜くのは楽勝ですが,動きが速くなると厄介ですよね!
温度が上がると抵抗が増える,これは結構重大な問題な気がしませんか?
なぜなら,抵抗はジュール熱によって勝手に発熱してしまうからです。
電気回路の問題を解くとき,私たちはいつも「この抵抗は10Ω(で一定)」という設定でやっていますが,厳密には「電流が流れるとジュール熱で抵抗の温度が上がるので,抵抗の値は増加していく」はず。
…でも安心してください。
普通の抵抗はよほど大きい電流を流さない限り,ほとんど温度変化しません。
いつもどおり「抵抗は一定」と考えて差し支えないのです。
なーんだ,じゃあ別にいいじゃん… って,ちょっと待った!!
確かに普通の抵抗はそう簡単に熱くならないけど,だいぶ熱くなる部品をみなさんは知っているはず。
そう,豆電球や白熱電灯です!
これらは手で触ってわかるほどの高温になりますよね?
さすがにそのレベルの温度上昇だと抵抗の変化を無視するわけにはいきません。
こういった “普通でない” 抵抗はどうしたらいいのでしょうか?
電球のI-Vグラフ
電球の抵抗値がどのように増加するのかグラフで見てみましょう。
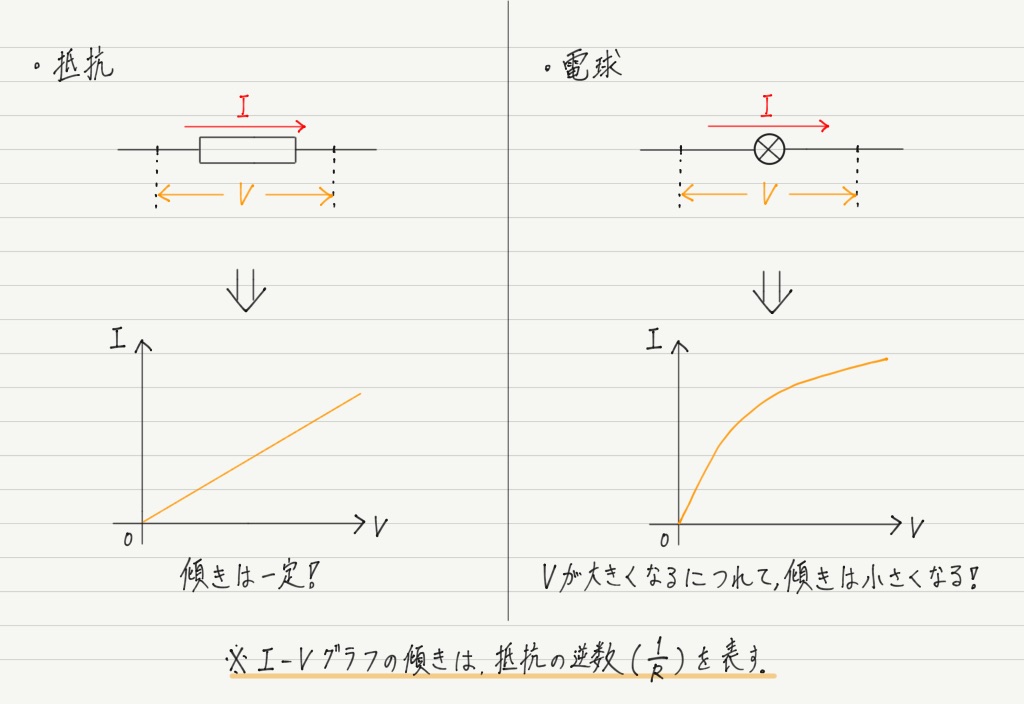
普通の抵抗のI-Vグラフは原点を通る直線,つまり電流と電圧が比例する形になっているので,オームの法則に従っていることがわかります。
一方,電球のI-Vグラフは直線ではないので,電流と電圧に比例関係はありません。
つまり電球は「抵抗のはたらきをもっているのに,オームの法則には従っていない」ことになります。
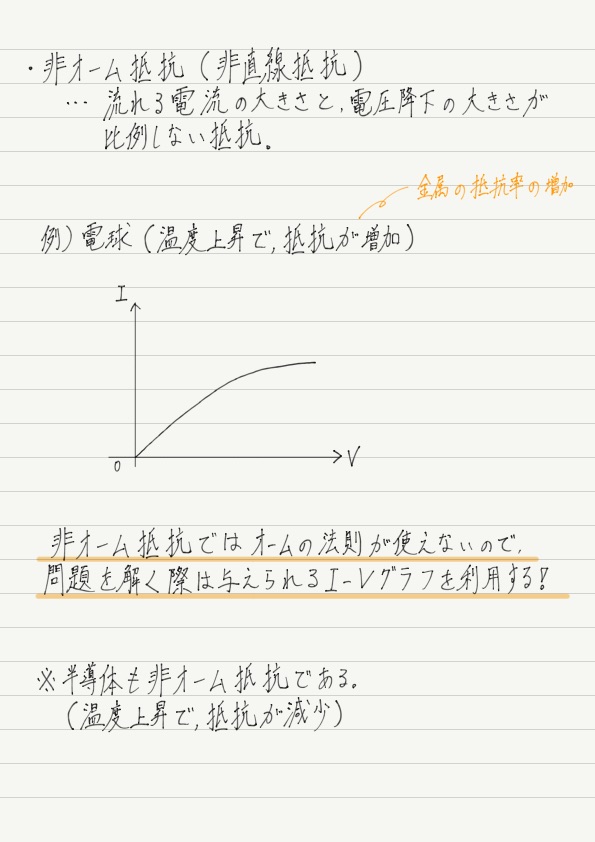
このようなオームの法則に従わない抵抗を,非オーム抵抗といいます。
(I-Vグラフの形が直線でないことから,非直線抵抗や非線型抵抗とも呼ぶ。)
非オーム抵抗を含む回路の問題
オームの法則に従わないということは,もちろんオームの法則を使って計算することもできないわけで,問題を解くときに困っちゃいます。
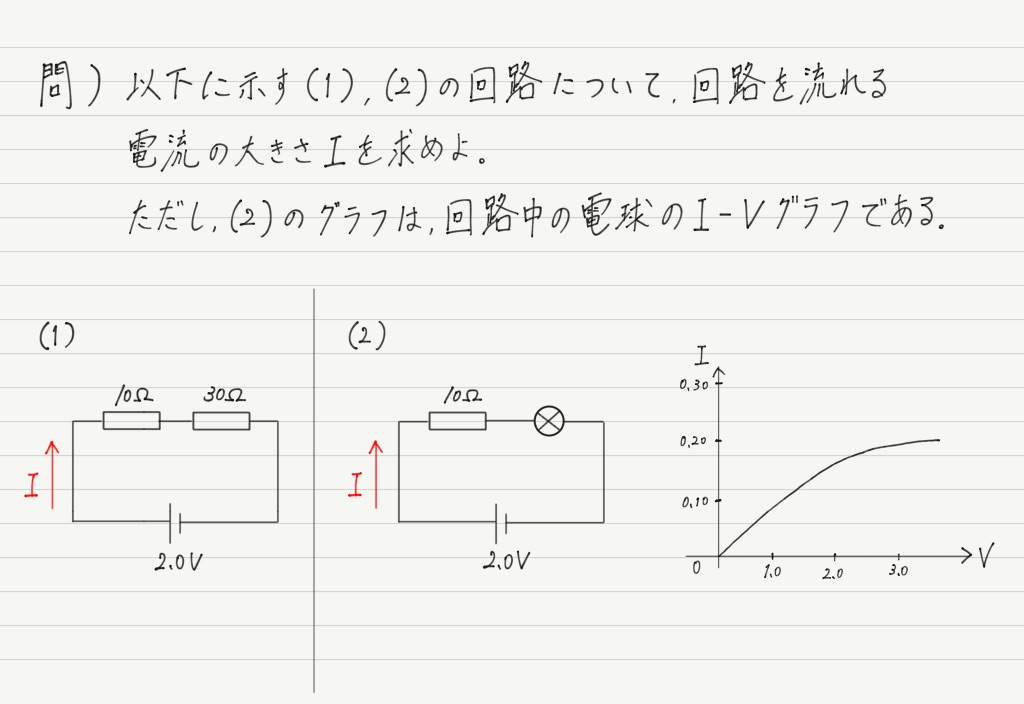
この問題の解法について考えてみましょう。
(1)は合成抵抗を使えば一発なのですが,(2)の話とつながりをもたせたいので,敢えて合成抵抗は使わずに計算してみます。
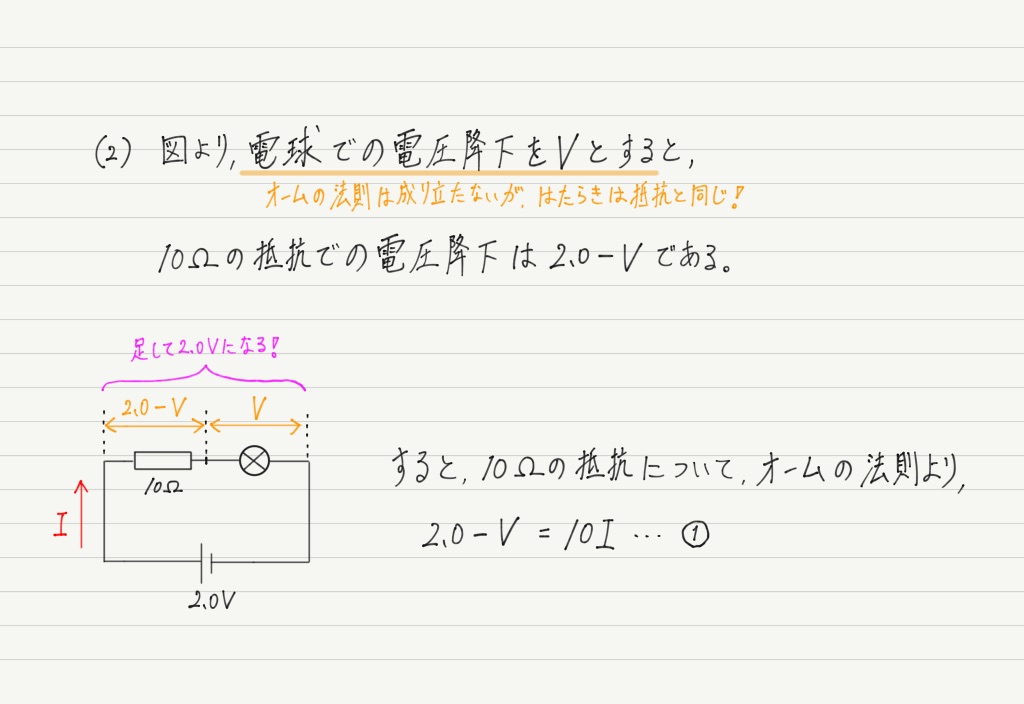
では,お待ちかねの(2)。
電球はさておき,普通の抵抗についてはオームの法則が成り立つので式を作っておきます。
VとI,2つの未知数があるので,これを解くためには式がもう1本必要です。
が,先ほどから言っている通り,電球ではオームの法則が成り立たないので式がつくれません。 こりゃ困った…
わからなくなったら基本に立ち返りましょう。
連立方程式の基本は中学校で学習したはずです。
さぁ,記憶を呼び覚ましてください… … …
ズバリ,今回の状況を打破するポイントは,「連立方程式の解は,2つのグラフの交点の座標」!!
これは連立方程式の基本中の基本。 この方法でまずは(1)を解き直してみましょう。
連立方程式を “解く” 代わりにグラフを書いて,その交点の座標を求めます。
このやり方は(2)でも使えそうですね!
電球ではオームの法則の式が立てられないので,連立方程式を直接解くのは不可能。
ですが,連立方程式の解はグラフの交点としても求められます。
そして,電球のI-Vグラフなら問題文ですでに与えられています!
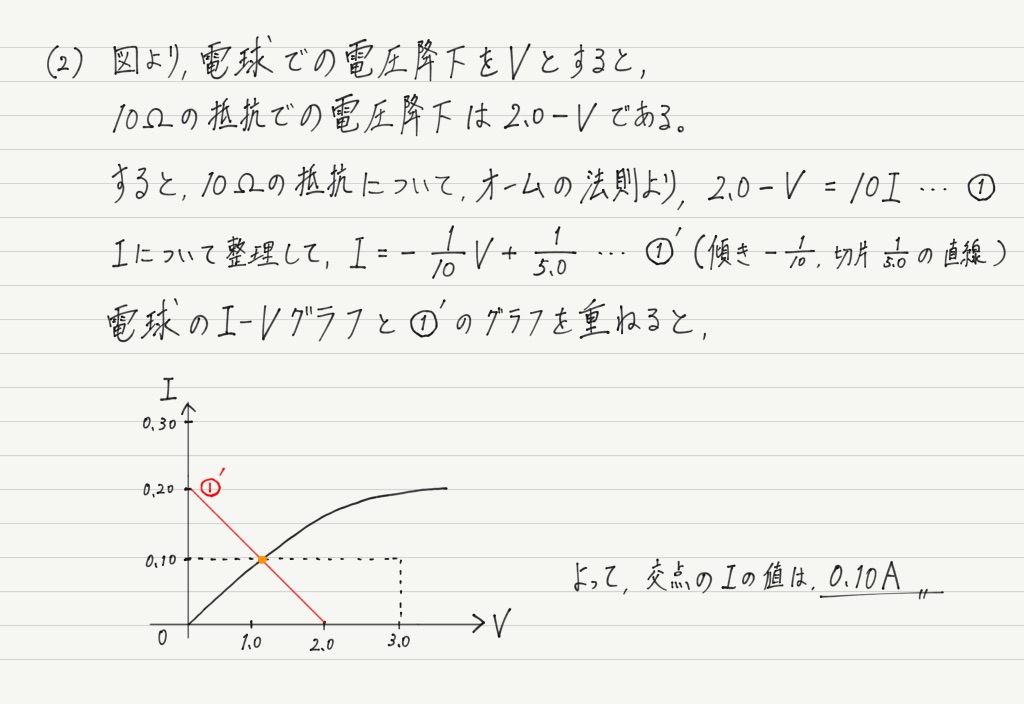
式がなかったらグラフを使えばいいじゃない,ということで,(2)はこう解いたらいいじゃない。
ちなみに電球以外の非オーム抵抗としては,ダイオードが挙げられます。
ダイオードの材料である半導体は,温度が上がると逆に抵抗値は下がるため,I-Vグラフの形は電球とは異なりますが,グラフの交点を求めるという手法は当然有効です!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください。 自分の手を動かすことが大事!