電気回路の主役は何といっても「回路を流れる電流」ですが,その正体は導体内部に存在する自由電子の流れでした。
…ということは自由電子の運動をあれこれ調べれば,電気回路に関する見識が深まるのではないでしょうか?
さっそく見ていきましょう!
電流について
ところでみなさん,「電流の大きさ」が何なのか覚えていますか?
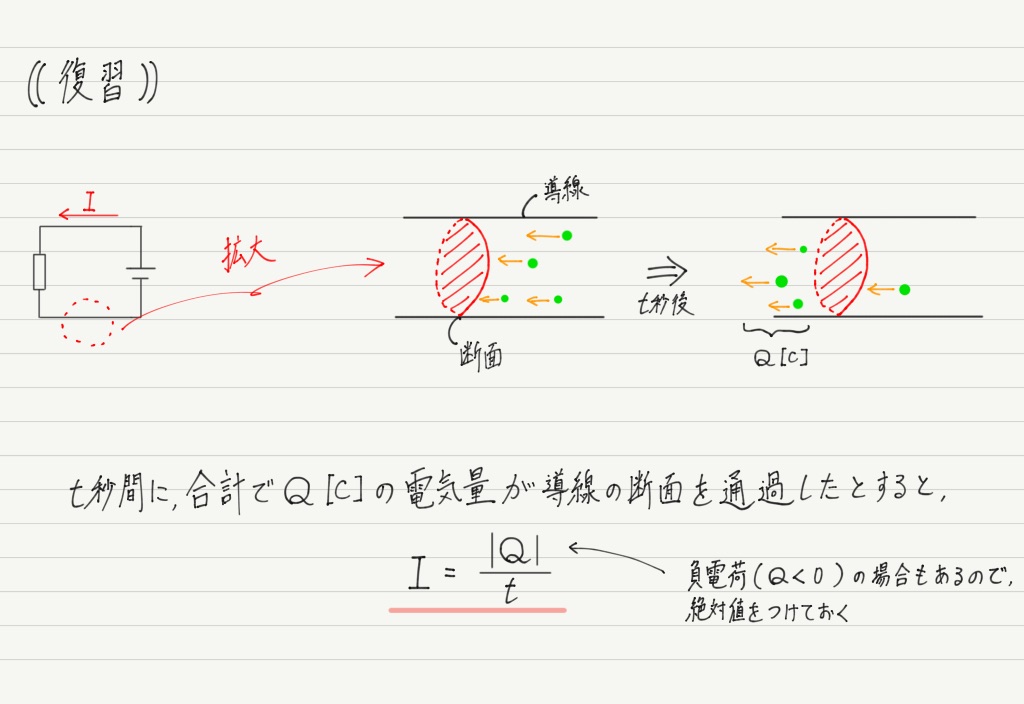
電流の大きさとは「導線の断面を,1秒間に通過する電気量の大きさ」を指します。
これを踏まえて,電子の運動という観点から電流を計算してみましょう。
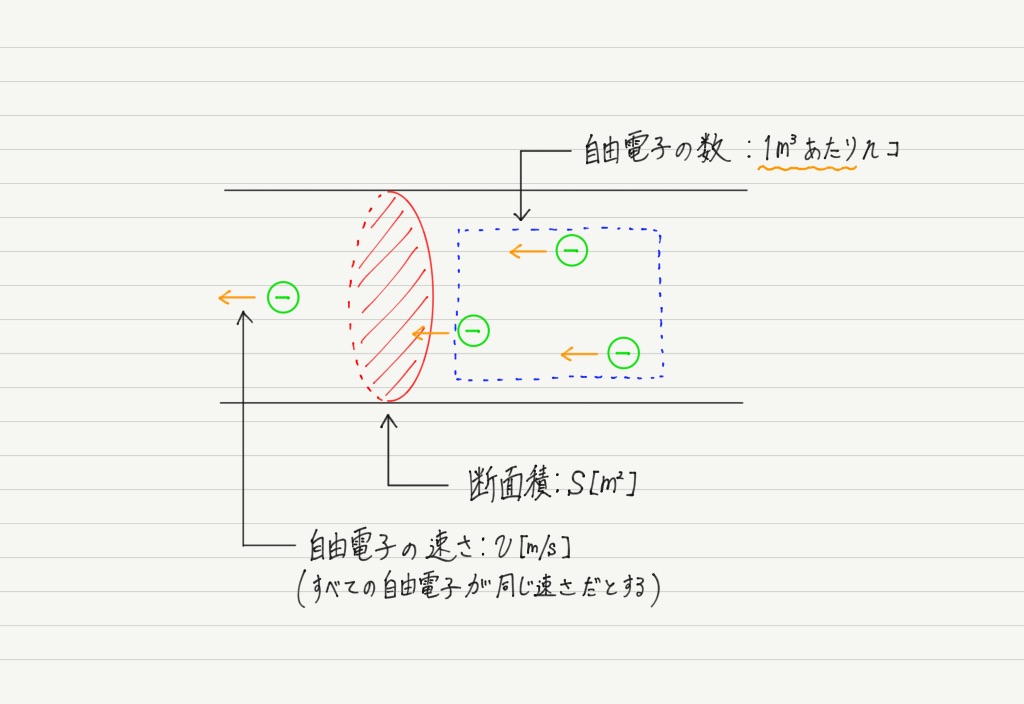
次のように設定します。
この状態で電圧をかけると自由電子が動き出します(=導線に電流が流れる)。
電流の大きさを計算するために知りたいのは,t秒の間に断面を通過する総電気量Qです。
Qが分かりさえすれば,あとはかかった時間tで割るだけで電流が求められます。
この方針を踏まえて計算へGO!
電流の大きさというおなじみの量を,「自由電子の速さ」という目に見えないミクロな量を使って表すことに成功しました!!
抵抗について
上の計算では自由電子の速さを一定としましたが,これについて詳しく考えてみましょう。
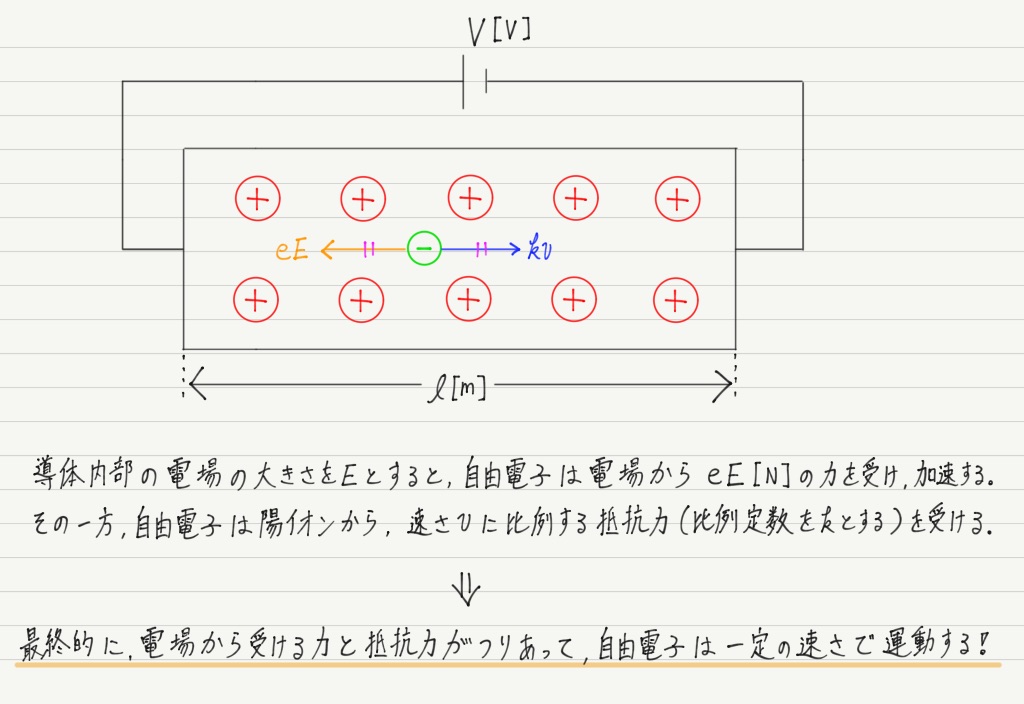
導体に電圧をかけたということは,導体内部に電場が生じていることに他なりません。
ということは,導体内部の自由電子はこの電場から静電気力を受けるはずです。
さらに導体内部には金属原子の陽イオンがあるため,衝突による抵抗力も受けます。
これをもとに計算を進めてみると…
この通り,抵抗と抵抗率の関係が出てきました!
物理基礎では抵抗を「通りにくい道」に例えて,イメージだけで「抵抗値は長さに比例し,断面積に反比例する」と説明していましたが,ミクロの視点を利用するとこのようにちゃんと計算で示すことができるのです。
すごい!
ジュール熱について
最後にジュール熱についても考えてみましょう。
これまたミクロの視点から考えると,「電子が電場からされた仕事が熱エネルギーになった」という結論が自然だと思われます。
これまた物理基礎で習ったおなじみの式に落ち着きましたね!
今回は電気回路に関するいくつかの概念をミクロな視点から捉え直してみましたが,大事なのはこれまで習ってきたことが計算によって裏付けされたということであって,式を覚えることではありません(よって,まとめノートはなし)。
ミクロな視点から現象を考えるというのは物理では非常に大事なので,このようなモノの見方にぜひ慣れてください。
時間に余裕がある人は,ぜひ問題演習にもチャレンジ! より一層理解が深まります。