前回は弦楽器(ギター)を例にとって,固有振動の考察をしました。
今回は同じ要領で管楽器を考察してみましょう。 管楽器はいろいろありますが,今回はリコーダーを例に説明します。 音楽の授業でみんな経験しているのでイメージしやすいと思います。
管楽器はなぜ鳴るのか
ギターの場合は弦が振動して音を出しています。 ではリコーダーは何が振動しているのでしょう?
リコーダー本体…ではないですよね?
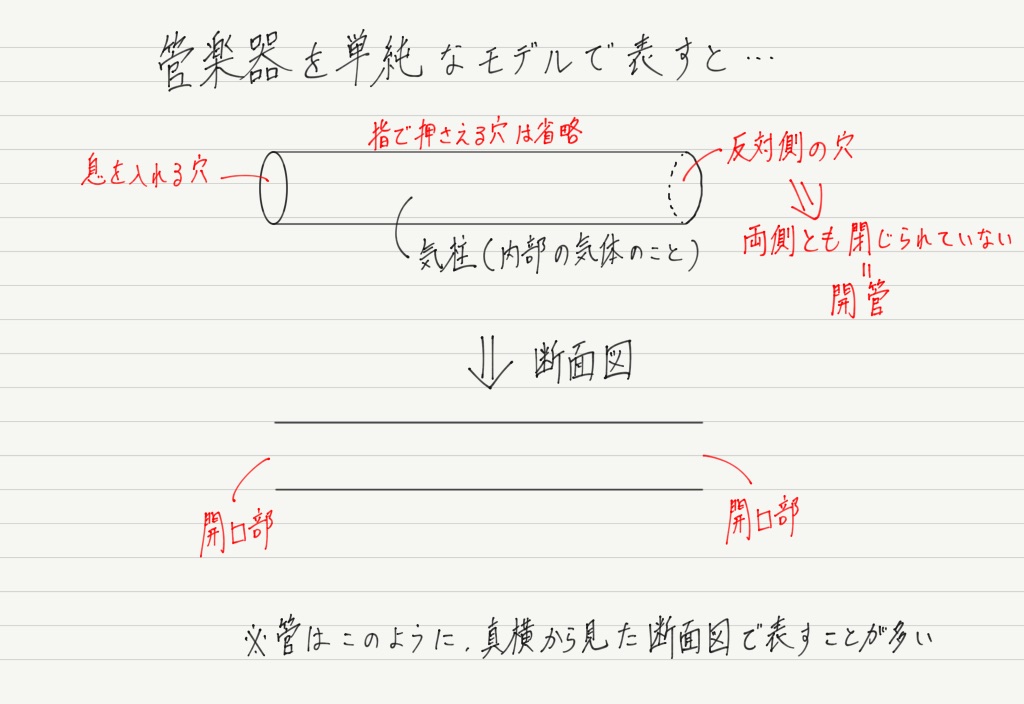
管楽器の形状を思い浮かべてください。 リコーダーに限らず,管楽器はどれも筒状,そしてその中には空気が充満しています。 もう分かりましたね?
管楽器は,楽器の内部の空気が振動しているのです!
筒の内部にある空気のことを気柱といいます。 管楽器のポイントは楽器の構造ではなくて,その中の気柱にあります。
では,気柱がどのような振動をするか見ていきましょう。
気柱の固有振動はどんな振動か
穴などを無視してリコーダーを簡単にモデル化すると,ストローのような筒になります。
このような,両側が開いている管のことを開管と呼びます。 リコーダーは片側から息を吹き込んで中の空気を振動させます。
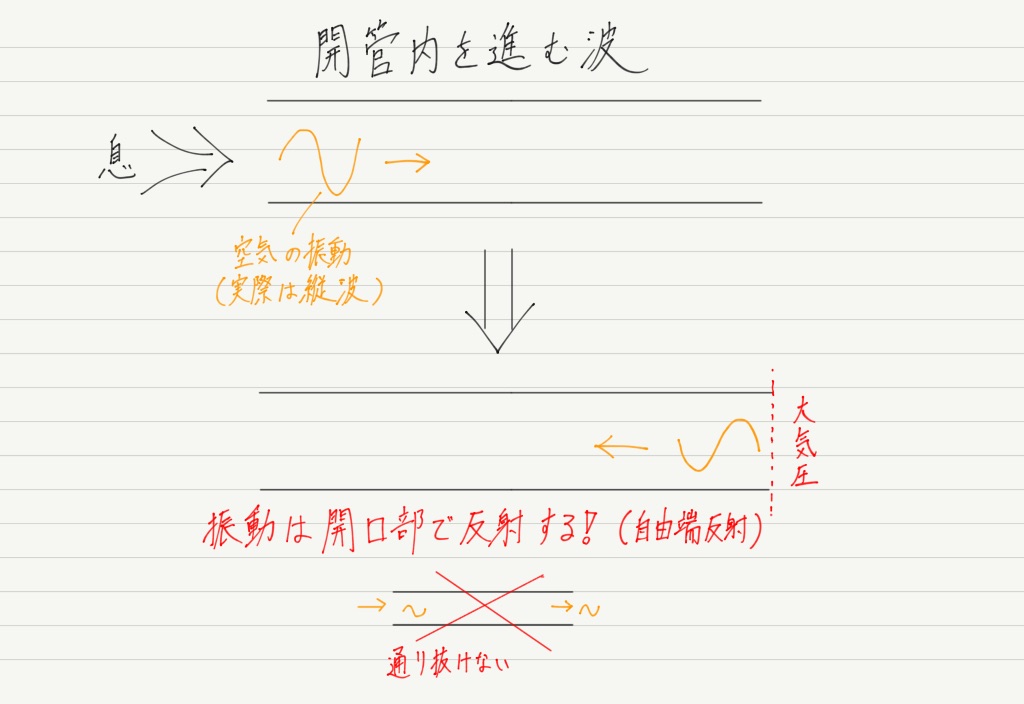
さて,気柱の振動を扱う上で重要なポイントがあります。 それは,振動は管の外に出ていかないことです。
開管は両側の口が開いているので,左側から来た振動はそのまま右へ抜けていくように思えます。
ところが実際は,管の出口で押し戻されるのです!
これは管の中と外の圧力差が原因で起こります。
結果,管の中で右向きに進む波(入射波)と押し戻された波(反射波)が重なり,定常波が生じることになります!
これで弦楽器の話とのつながりが見えてきました。 弦楽器だろうが管楽器だろうが,その根底にあるのは定常波なのです。
ところで,弦に生じる定常波は両端が節でした(弦が両端で固定されているため)。
開管の場合,開口部では空気が自由に振動できる(=自由端反射)ので,その部分は定常波の腹になります。
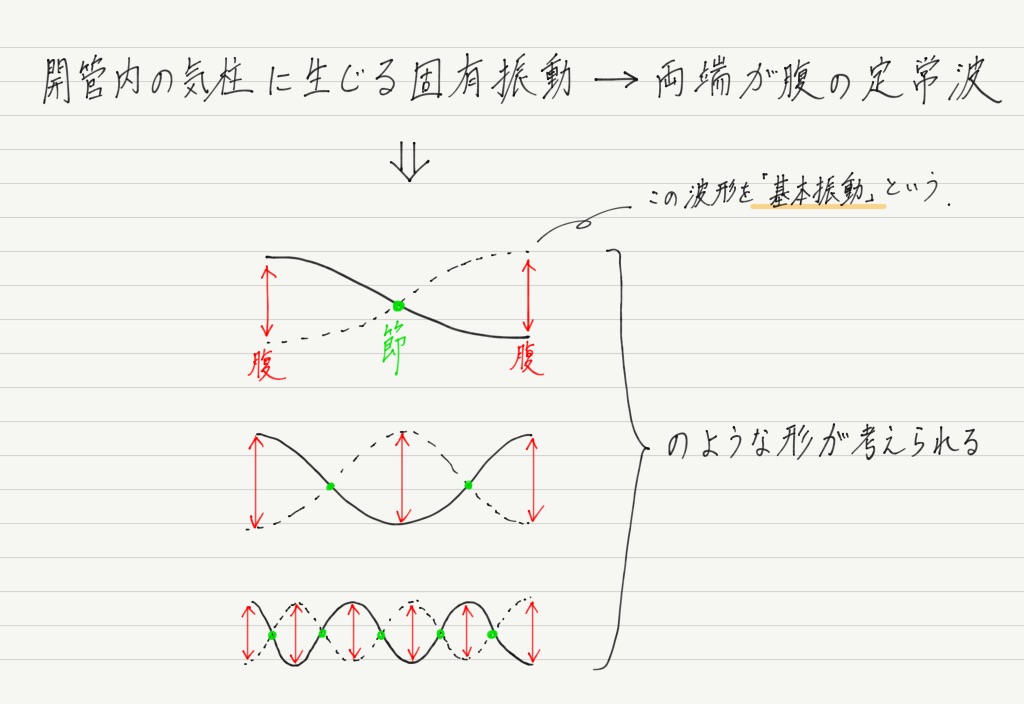
つまり,開管内の気柱の固有振動=両端が腹の定常波です!
開管内の固有振動の種類
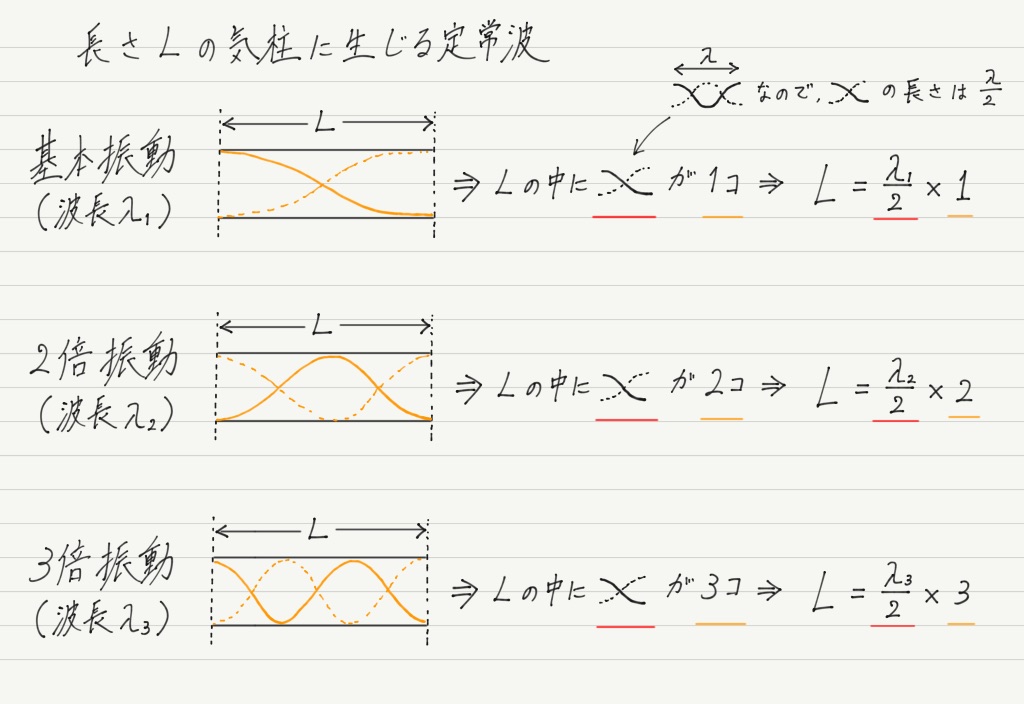
両端が腹の定常波ということは,たとえば次のような形が考えられます。
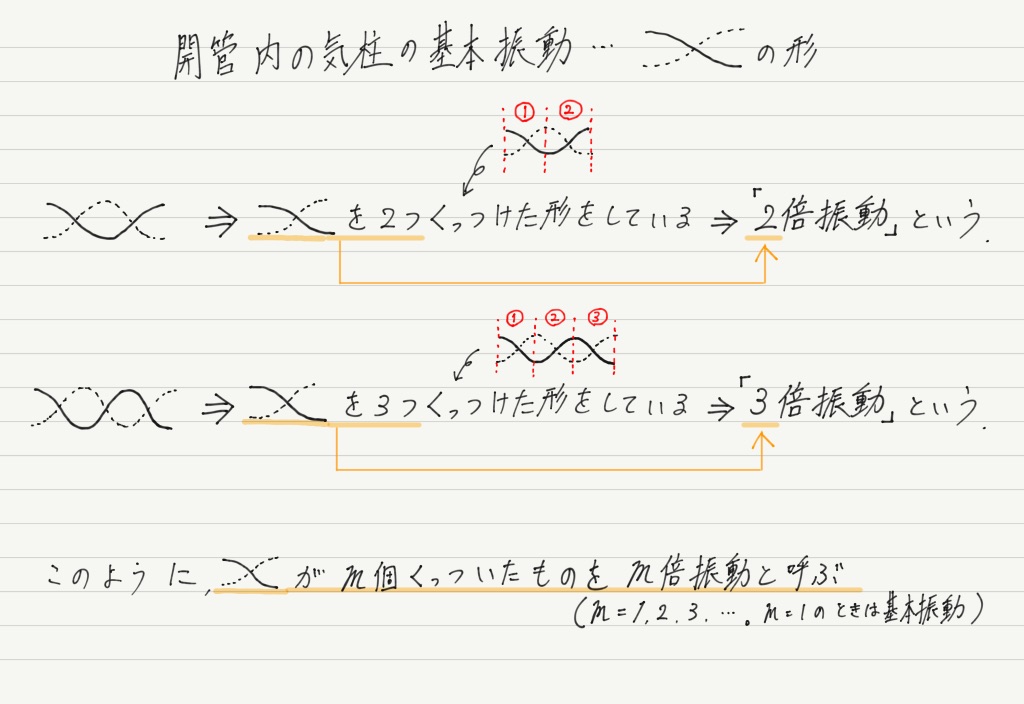
弦と同様,複数の定常波のパターンが考えられますが,一番シンプル(腹と節の数が最少)なものを基本振動と呼ぶこと,
それから,基本振動の形を m 個くっつけた形の振動をm 倍振動と呼ぶことは弦と同じです。
管楽器の内部ではこのような振動が混ざりあって,その楽器固有の音を出しています。
開管内の固有振動の考察
定常波の形がわかったところで,弦と同じように固有振動数を求めてみましょう!
気柱の長さを L[m]として,基本振動,2倍振動,3倍振動について考えてみます。
両端が腹になって,基本振動の形が変わったこと以外は弦の場合と同じ要領です!!
ここまで来たらあとは波の基本式を使うだけ。
弦の固有振動と式の形はそっくりですが,式に登場する波の速さに注意してください!
気柱の場合,Vは気体を伝わる波の速さを表します。 つまり音速です!
弦の固有振動の式にあったvは音速ではなく,弦を伝わる波の速さなので注意してください。
(音の分野だから,という先入観で間違えやすいです)
m 倍振動(m = 1,2,3,…)の場合も計算してみましょう。
弦と同様に,m 倍振動の固有振動数が基本振動のm 倍になっていることがわかります。
この式は自力で導けるようにしておきましょう!
固有振動数からみる管楽器のしくみ
弦の場合,固有振動数は弦の長さと波が伝わる速さで決まりましたが,管の場合,波が伝わる速さは音速で一定なので,固有振動数は気柱の長さだけで決まります。
(息を強く吹き込んでも,振幅が大きくなるだけで伝わる速さは変化しません!)
気柱の長さLは分母にあるので,固有振動数は気柱の長さに反比例します。 気柱が長いほど,振動数は小さくなる(=低音)。 低音の楽器ほど巨大になる理由ですね!
また,トロンボーンは管を出し入れすることで,管の長さを変化させて音階を変えています。
ではトロンボーン以外の楽器はどうやって音階を変えているのでしょう?
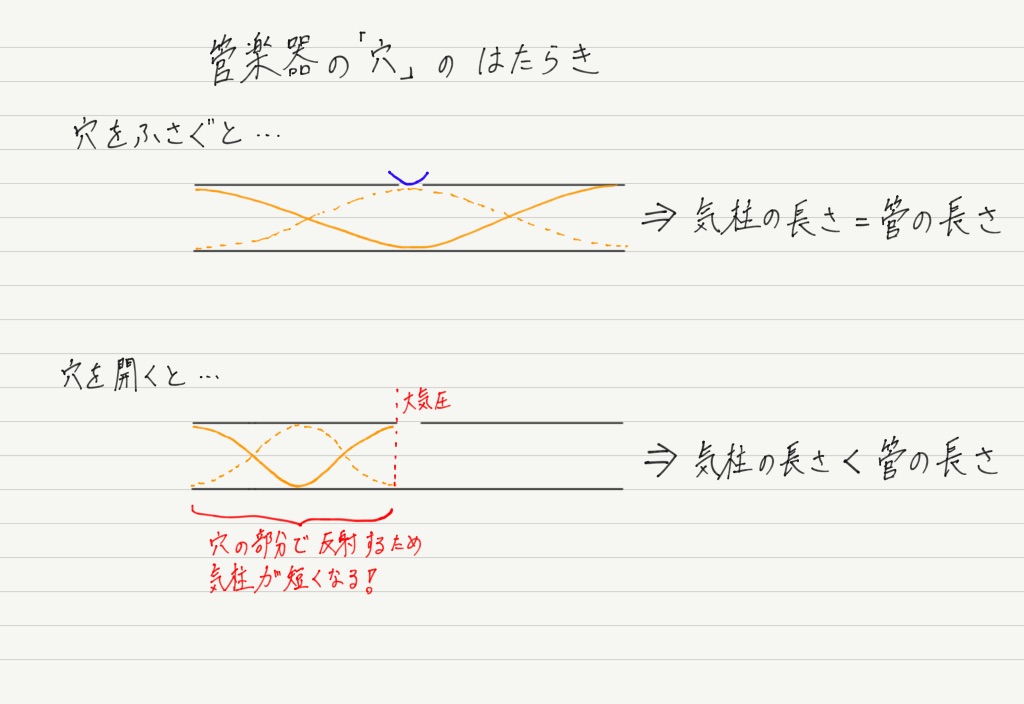
リコーダーは演奏中に長さが変わることはありません。 ポイントは,式の中のLが “管の” 長さではなく,“気柱の” 長さであることです。
リコーダーやその他管楽器は,本体に開いた穴を開けたり塞いだりして音階を変化させています。
穴を開けたままにするとその部分で波が反射するので,楽器自体の長さを変えずに気柱の長さだけを変化させることができます。
穴をすべて塞ぐと楽器の長さをめいっぱい使うことになるので,それがその楽器が出せるもっとも低い音になるということも理解できますね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回は両側が開いた管でしたが,次回は片側だけが開いた管について見ていきます!