〜物理初学者あるある〜
物理の問題を解く。
よし,答えは2mだな。
解答を見る。 えっ? 2.0m?
その「.0」いる!?!?!?
今回の記事ではそんな初歩的な疑問にお答えします。
測定の誤差と有効数字
何かを測定するとき,そこには必ず誤差が生じます。
ものさしで長さを測ってみたら4.5cmと4.6cmの間だった,みたいなことありますよね?
ものさしは普通1mm間隔で目盛りがふられているので,それ以下の長さは正確には読み取れません。
もちろん長さ以外の測定でも誤差はつきもの。
理科では測定した値が「真の値」からどれだけずれているかを常に考慮しておく必要があります。
ここで最初の話に戻りましょう。
実は「2m」と「2.0m」のちがいは,測定の誤差にあります。
・測定値が「2m」→ 長さは1.5m以上,2.5m未満と解釈される
・測定値が「2.0m」→ 長さは1.95m以上,2.05m未満と解釈される
ほら! 2mと2.0m,全然意味がちがうでしょ!?
さらに0を付け足して2.00mと表記した場合は,1.995m以上,2.005m未満を意味します。
さらに精度が上がっていますね!
2m,2.0m,2.00mのちがい,つまり「その数値にどれだけの誤差があるか」を表すのに,理科では有効数字という考え方を用います。
その言葉を使うと,2mは有効数字1桁,2.0mは有効数字2桁,2.00mは有効数字3桁と表されます。
有効数字の桁数が多いものほど,より正確に測定したということです。
有効数字の桁数の数え方
問題を解いていると「有効数字◯桁で答えなさい」という問題に遭遇します。
この問題に正しく答えるためには,まず有効数字の桁数の数え方を知る必要があります。
簡単なので確実にマスターしてください!
これが基本のルール。 ここだけ見るとめっちゃ簡単そうですが,例外もあります。
慣れていないとまちがえやすいので要注意!
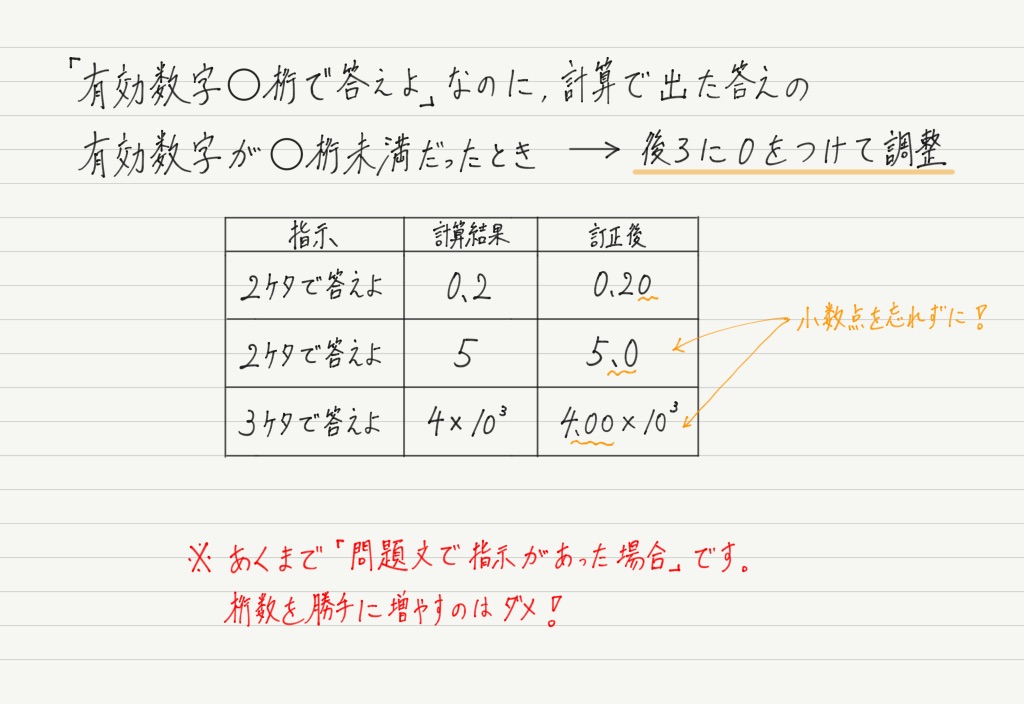
「有効数字◯桁で答えよ」のやり方
桁数が読めるようになったら,次は問題文で指定された桁数に合わせる方法をマスターしましょう。
そして次が一番よく使うパターンです。
10の累乗もよく使います。
最後にもう1つだけ。
これぐらいのことがわかっていれば,まずは大丈夫!
測定値の計算と有効数字の桁数
問題集を見てもらえばわかりますが,「答えは有効数字◯桁で答えよ」と書いていない問題も多いです。
コレ,初学者は勘違いしがちなんですが,何も書いてないのは「有効数字は適当でいいよ」という意味ではなく,「何桁にするかは自分で察しろよ」っていう意味です。
計算における有効数字の取り扱いには自動的に次のルールが適用されます!
これらのルールはあらかじめ知っておかないと減点不可避…
問題演習を通じて,しっかりと頭に入れておきましょう!