オームの法則は1つの抵抗に対して成り立つ法則なので，回路内に抵抗が複数個ある場合には，原則として「抵抗の数だけオームの法則を用いる」ことになります。 問題を見て抵抗が3つ含まれていたら，「ああ，3回オームの法則を使うんだな」と思ってください。
では抵抗が200個含まれていたら，200回オームの法則を使うのでしょうか？
答えはYES。 200回使ってください。
まぁ，物理の問題としては多くてもせいぜい4つぐらいだと思うのでそんな膨大な計算の心配はいりませんが，それでも数が多くなるとさすがに面倒ですよね(^_^;) もうちょっとうまい方法はないのでしょうか？
合成抵抗という考え方
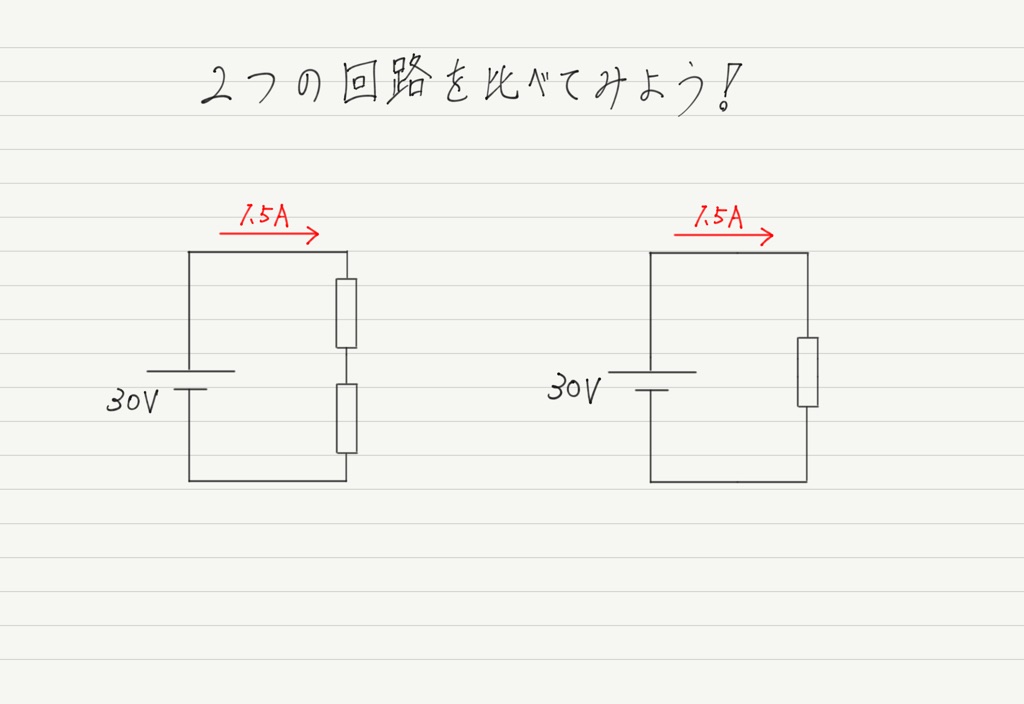
まず，この図を見てください。
回路としては別物ですが，「30Vの電源を接続したら，1.5Aの電流が流れた」という点では一致しています。
「同じ電圧をかけたら同じ電流が流れた」ということは，左の回路の2つの抵抗と，右の回路の抵抗は同じはたらきをしているといえるでしょう。
このように複数の抵抗をまとめて，同じはたらきをする1つの抵抗（合成抵抗という）に置き換えて考えると計算がとても楽になります。 抵抗が1つならオームの法則は1回使うだけで済むからです！！
問題は，何Ωの抵抗に置き換えればいいのか？というところですが，それはもとの抵抗たちから求めることができます。 さっそく求め方を紹介しましょう！
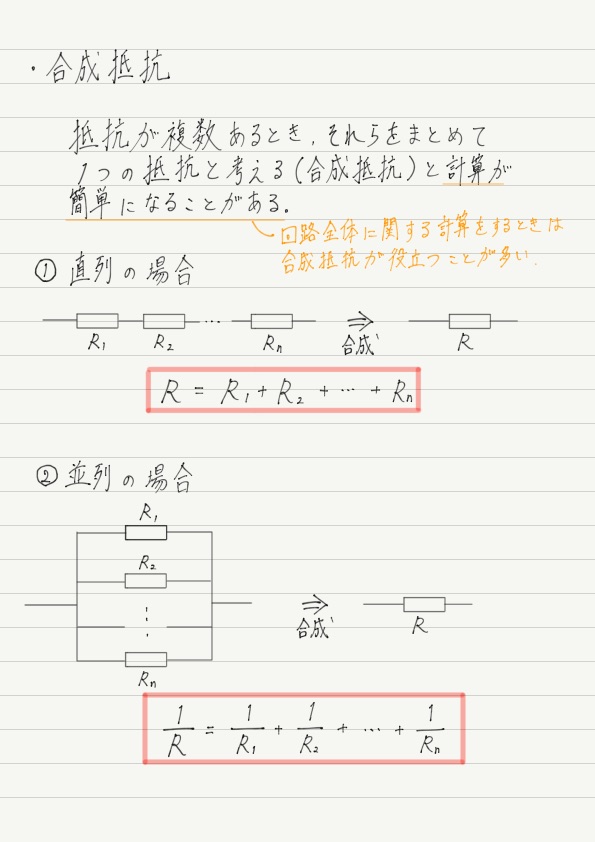
直列に接続された抵抗の合成
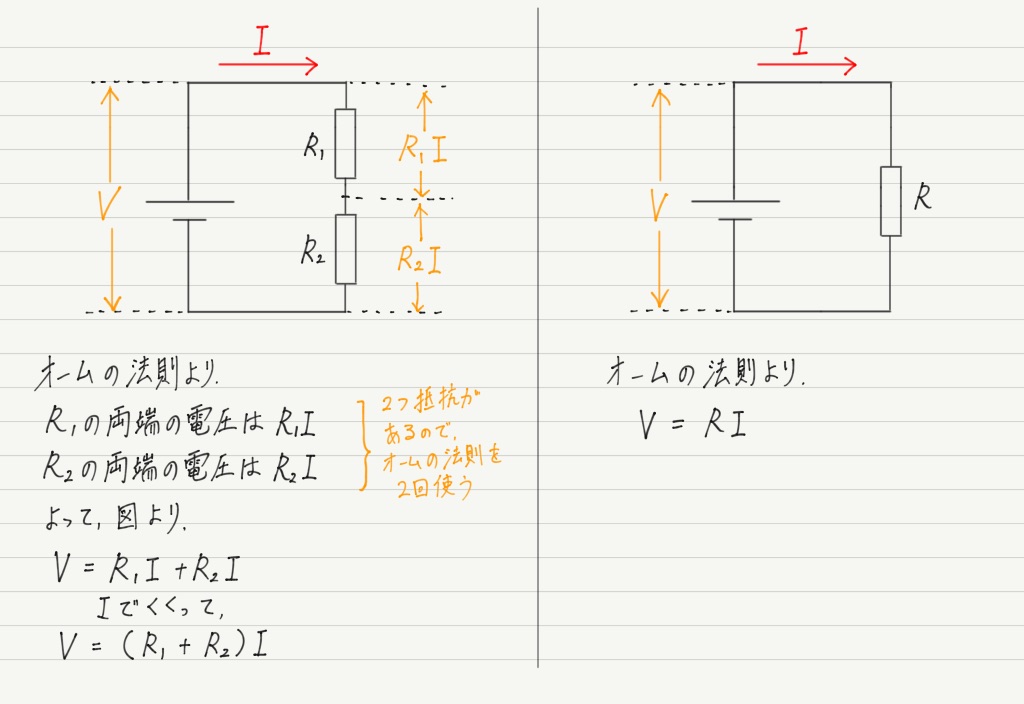
まず先ほどと同じように，抵抗が2つある回路と，それを合成抵抗で置き換えた回路の2つを用意して比べてみましょう。 それぞれでオームの法則を用いて計算してみます。
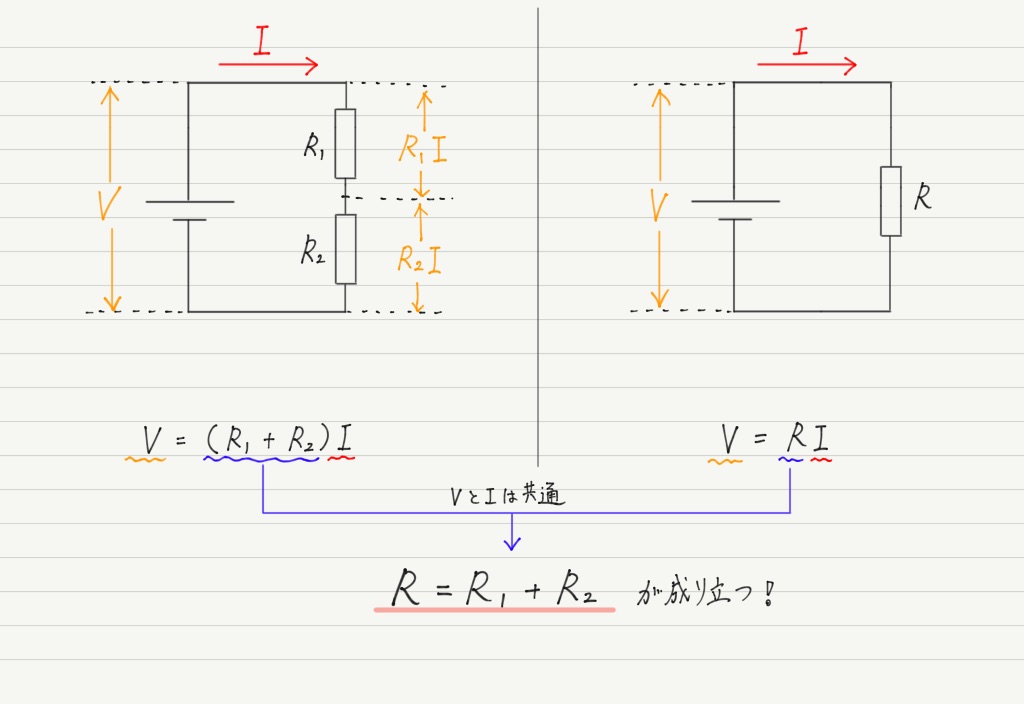
この2つの回路は抵抗の数はちがいますが，同じはたらきをする抵抗で置き換えたものなので，2つの式は同じにならなければいけません。 得られた式を比較してみると…
これが合成抵抗Rを求める式です！ 抵抗が直列につながれている場合は，このようにそれぞれの抵抗の値をただ足すだけで合成抵抗の値が得られます。
抵抗が3つ以上の場合もただ足すだけでOK。
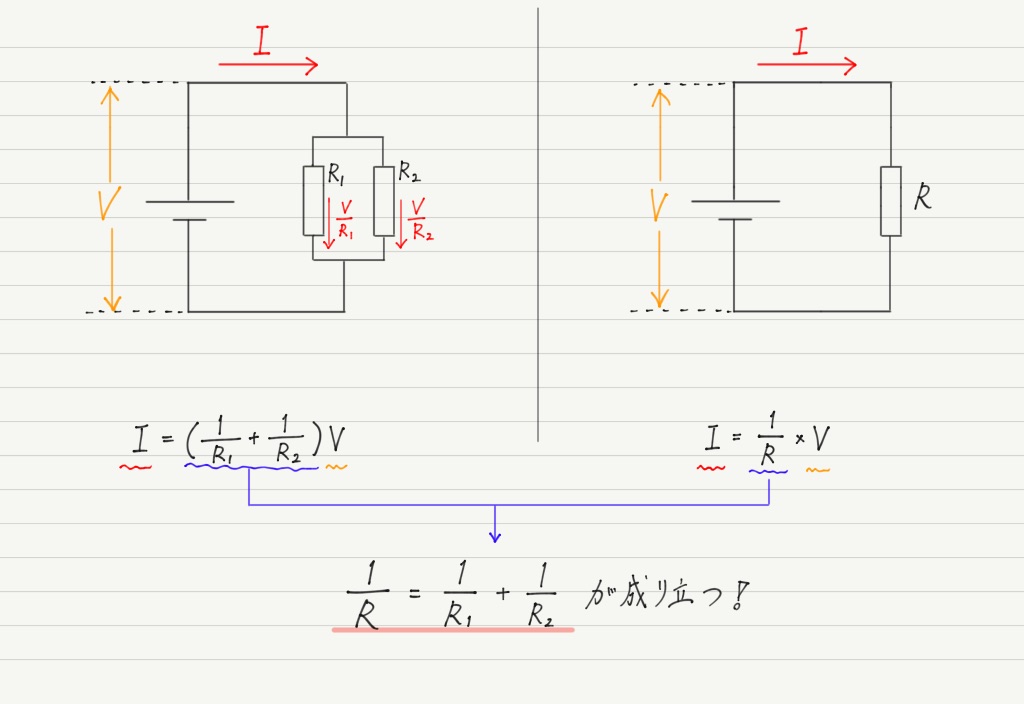
並列に接続された抵抗の合成
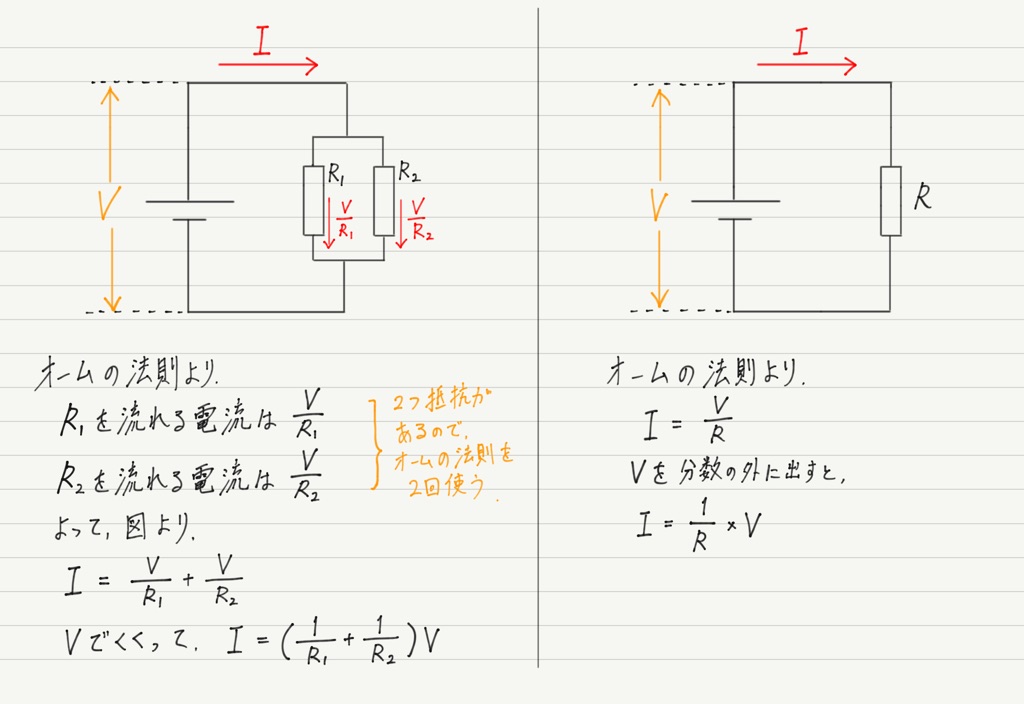
直列の場合と同様に，それぞれでオームの法則を用いて計算してみましょう。
式を比較すると…
これが並列の合成抵抗です！ 抵抗が並列につながれている場合は，それぞれの抵抗の逆数をとって足したものが，合成抵抗の逆数になります。
抵抗が3つ以上の場合も逆数をとって足せばOK！
「“和”分の“積”」は万能ではない
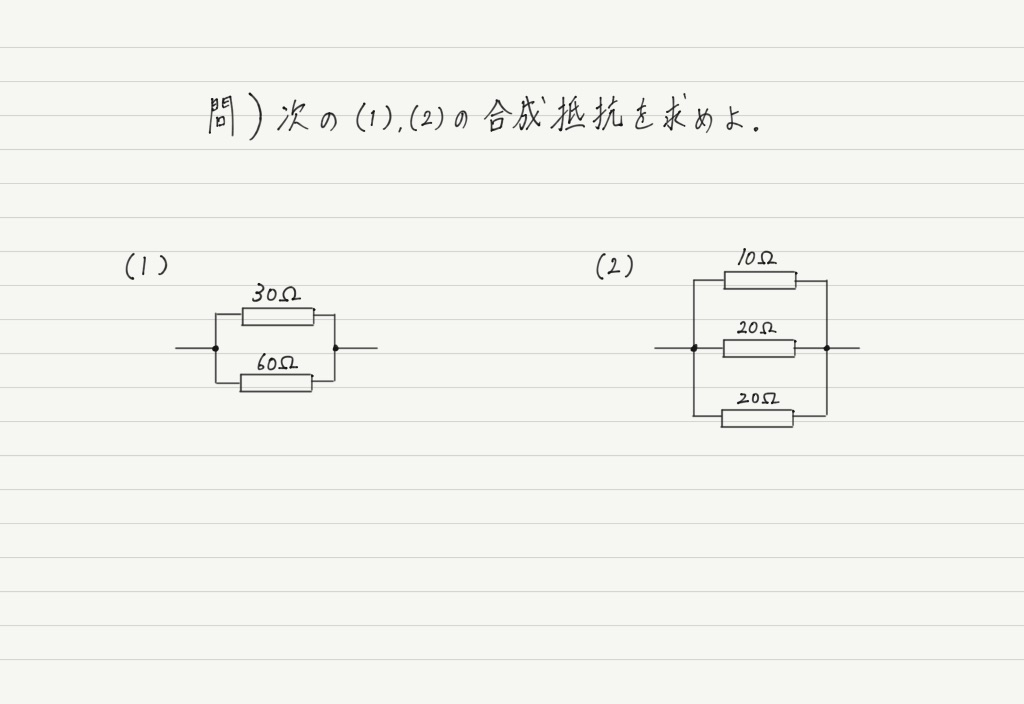
直列の場合は問題ないと思いますが，並列はちょっと面倒なので，一度計算練習をしてみましょう。
このあとに答えを載せますが，一度自分で計算してから見てください。
解答はこちらです。
逆数をとって，通分して足すところまではできるけど，最後それを逆数に直すのを忘れる，というのは初心者によくある間違いです。
ここで1つ注意。 並列の合成抵抗の求め方として，「“和”分の“積”」という公式を教わった！ という人が一定数います。
この計算を習った人たちからは，「こっちのほうが通分とかしないから簡単だよ？」「なんでわざわざ逆数をとったりするの？」という意見が飛び交うのですが，実は「“和”分の“積”」の公式は万能ではありません！！
例えば(2)は，“和”分の“積”では求められません。
「“和”分の“積”」は，抵抗が2つのときにしか使えません。 一方，逆数をとる方法は抵抗が何個であっても可能です（通分は面倒になるけど笑）。
そういう事情があるので，残念ですが「“和”分の“積”」派の人は，今後は逆数派にシフトしてください。
合成抵抗は万能ではない
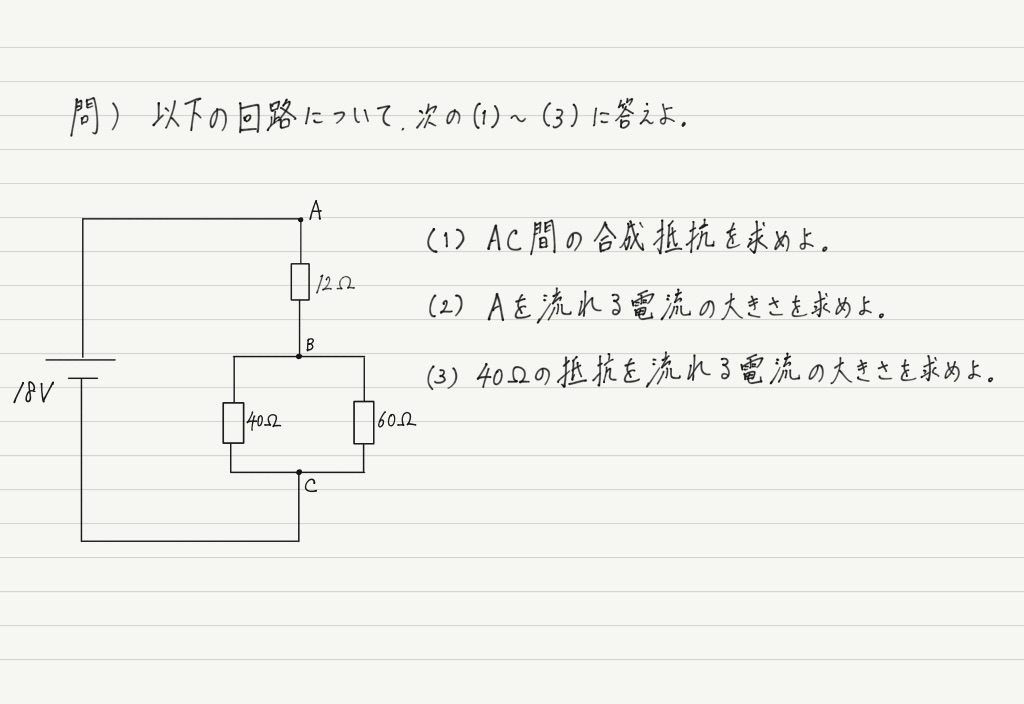
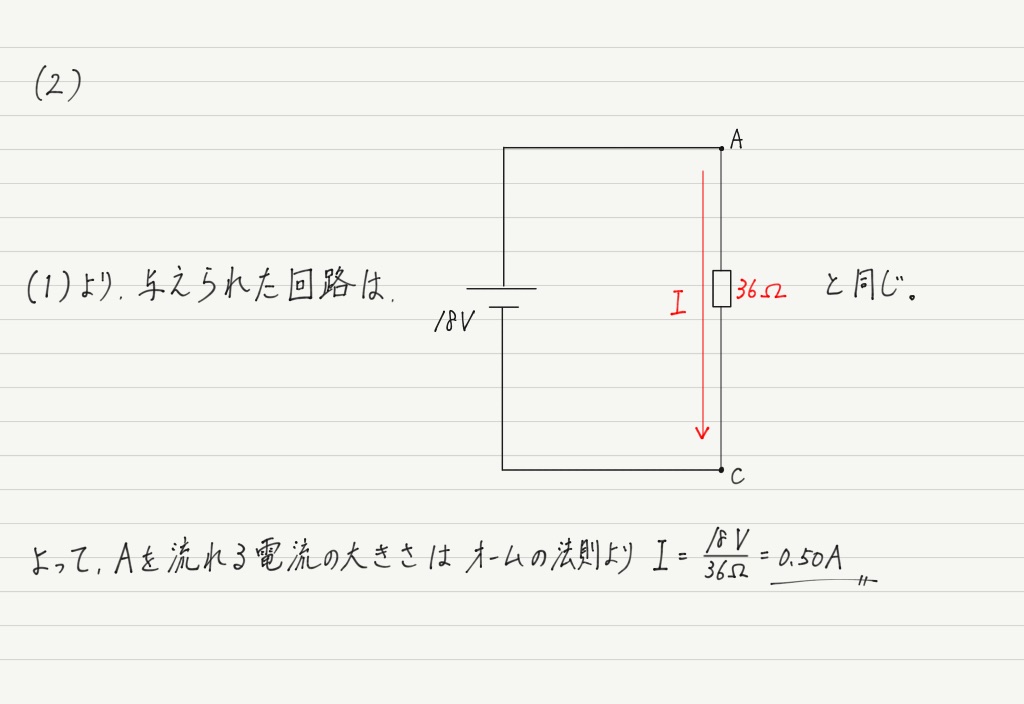
最後に練習問題をやってみましょう。
答えはこの下にあります。
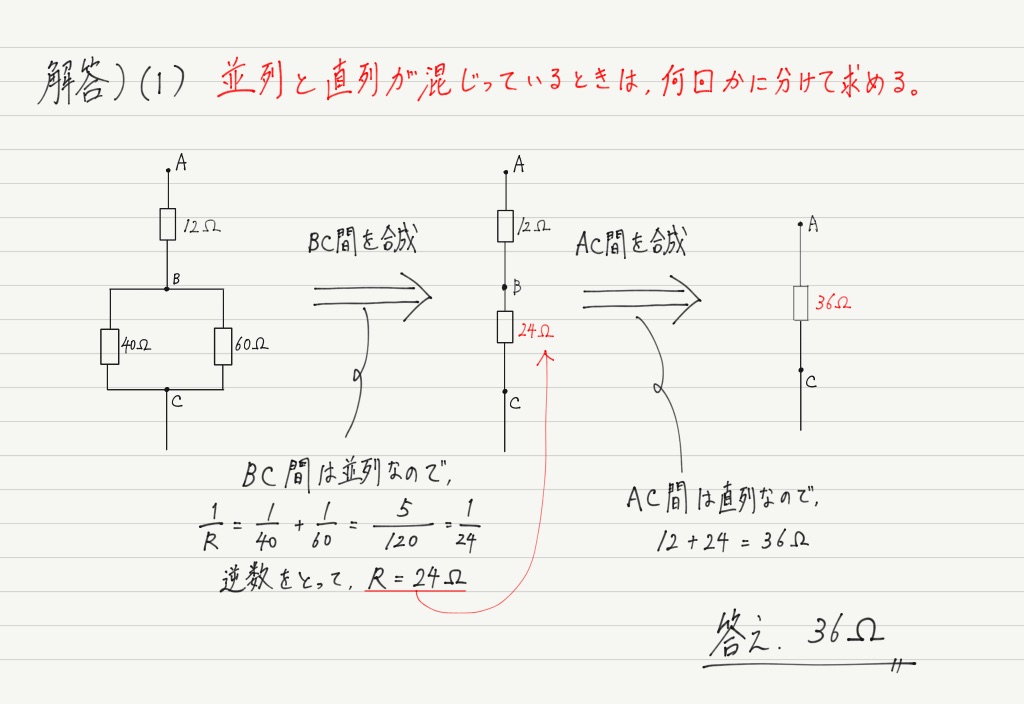
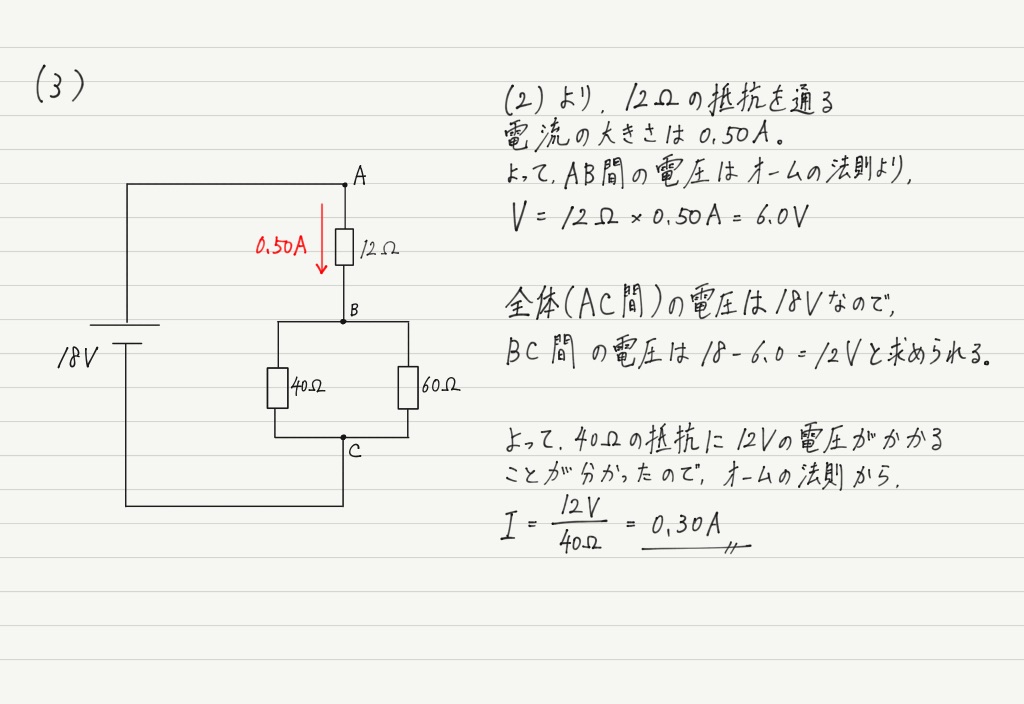
最後の問題は合成抵抗を使っていたのでは解けません。
合成抵抗は回路全体の計算をするとき（電流の大きさや消費電力など）は大きな威力を発揮しますが，個々の抵抗に関する計算にはまったく使えません。
そもそも合成抵抗はあくまでも計算を簡単にする道具に過ぎません。 なんなら合成抵抗を使わなくても回路の計算は可能です。
抵抗が複数あったらとにかく合成！ではなく，合成したほうが簡単になるのか，合成しないほうがすんなり計算できそうか見極めて，臨機応変に対応できるようにしましょう！
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
