物体を変形させたり，運動の状態を変えたりするためには力が必要ですが，直接にしろ，道具を使うにしろ，ふつうは対象に触らないと力を加えることはできません。
ところが前回登場した静電気力は，電荷どうしが離れていてもお互いに力を及ぼしあいます。
「静電気力とは例外的にそういう性質をもっている」と割り切ってしまうのも一つの手かもしれませんが，イマイチ腑に落ちませんね(^_^;) あまり例外を認めたくないという気持ちもあります。
というわけで今回は，離れていても静電気力がはたらく理由について考えてみましょう。
離れている「ように見える」だけ！？
例外を認めたくないということは要するに，静電気力も他の力と同じように，“直接触れて” 力を及ぼしていると考えたい…！ということです。
離れていてもはたらいているように見えるけれど，直接力を受けていると考えたい…
メチャクチャなことを言っているように聞こえますが，解決法は簡単（？）。 電荷の間に「目には見えない何か」があると考えればよいのです！！
この “何か” を電場（電界）と呼びます。
（※物理系の人間は「電場」，電気工学系の人間は「電界」と呼ぶことが多いです。 英語では，“electric field” なので，「場」が本来の訳です。「界」だったらworldじゃん？）
電場を用いた静電気力の説明
電場という概念を使わなければ，「静電気力は離れていてもはたらく力で，向きは電荷の符号の組み合わせで決まり，大きさはクーロンの法則に従う」でおしまいです。
電場を用いた場合，この現象はどう解釈されるのかを見ていきましょう。
こうすれば，電荷と電場は直接触れているので，「静電気力も他の力と同じように，接触しているものから受ける力である」と考えることができます！！
え？ こじつけっぽいって？
確かに，目に見えない存在を持ち出すのはこじつけに感じますが，それを言うなら，たとえばエネルギーだって目に見えるものではありません。
ですが，もうご存知の通り，エネルギーという概念はいろんな現象を説明できるとても便利な概念です。 目に見えなくとも，それで現象が矛盾なく説明できるなら問題ありません。
それに，電場と似た概念である磁場（磁界）については中学校で学んでいるはずです。 磁場も電場同様，目に見えませんが，砂鉄を磁石の周りにふりまくと，砂鉄が線に沿って並びます。 砂鉄が規則的に並ぶというのは，空間に “目に見えない何か” がある証拠で，それこそが磁場。
電場は砂鉄では検出できませんが，磁場同様，直接目に見えなくとも実在するものです。
電場の向きと大きさ
話がそれてしまったので，元に戻しましょう。
電場という概念を使うと，静電気力が接触して受ける力として扱えることは分かりましたが，力の向きや大きさについても矛盾なく説明できるようにしてあげないといけませんね(^^)
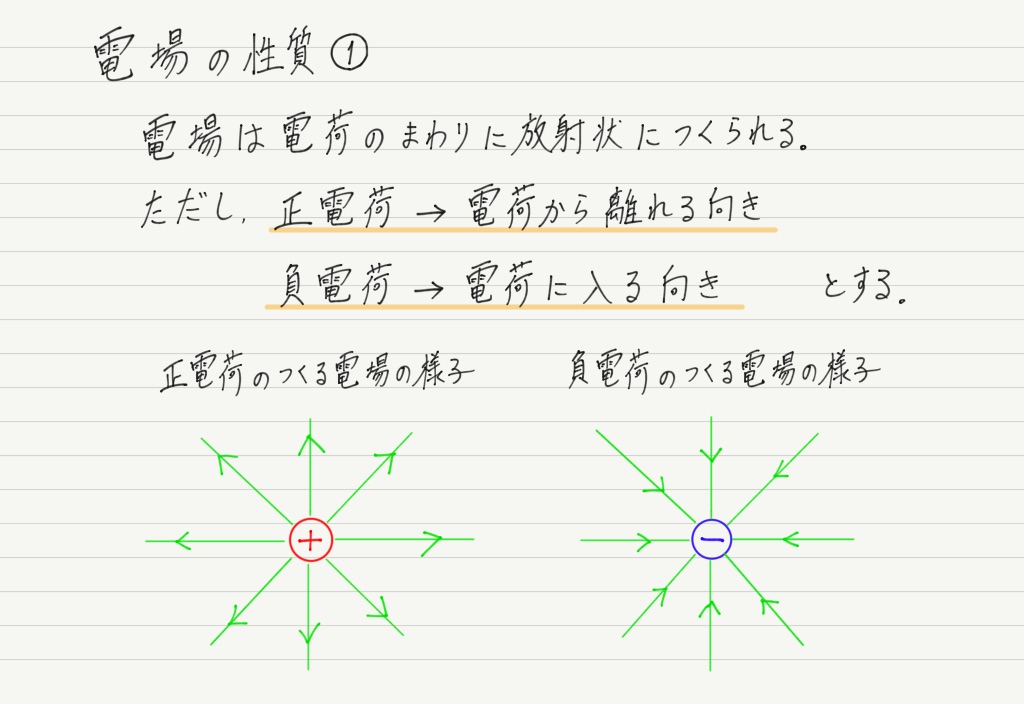
そのために，電場には以下のような性質があるとします。
このように考えれば，静電気力の向きの問題も，大きさの問題もすべて解決！
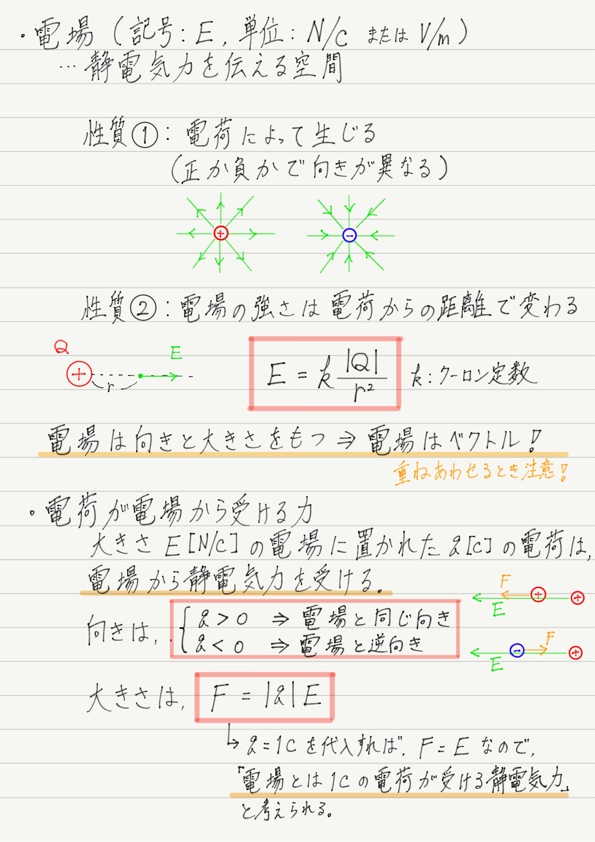
…ですが，上の説明で電場の “向き” と “大きさ” を導入したことに注意してください。 向きと大きさがあるということは，電場はベクトルです。
ベクトルってことは足し算するときなど注意が必要ですね！ さっそく練習問題いってみましょう！
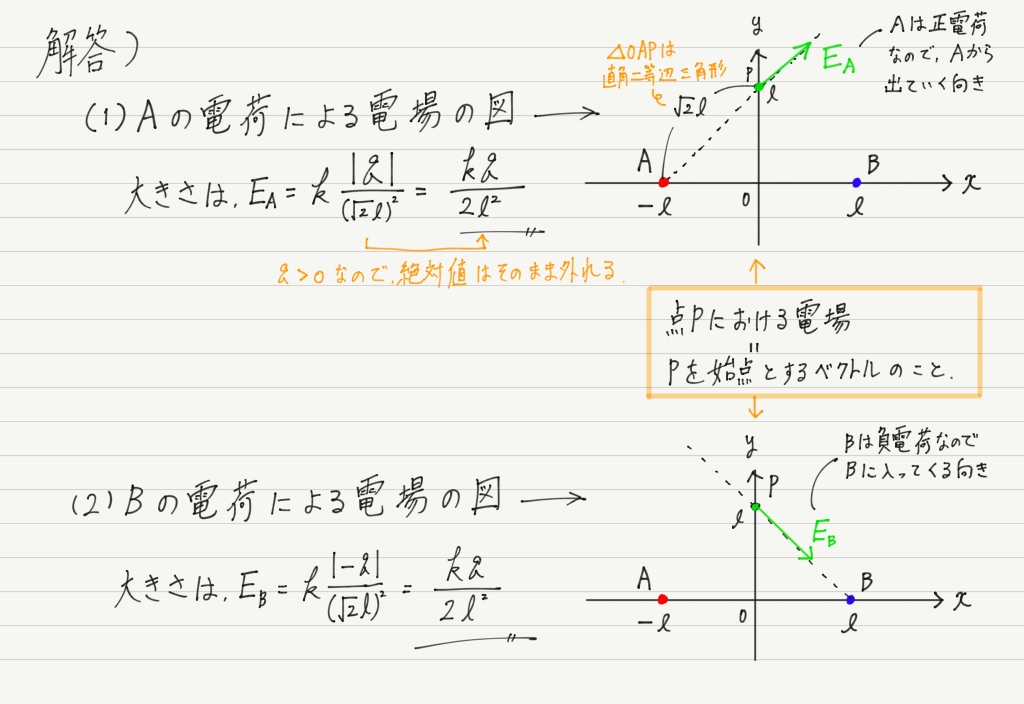
例題
ここまで単に「電荷」と言ってきましたが，今回の問題のように，ある1点に電気量が集まっているものを点電荷と呼びます。 たとえば，電子や陽子は点電荷とみなせます。 よく使われる言い回しなので，覚えておいてください。
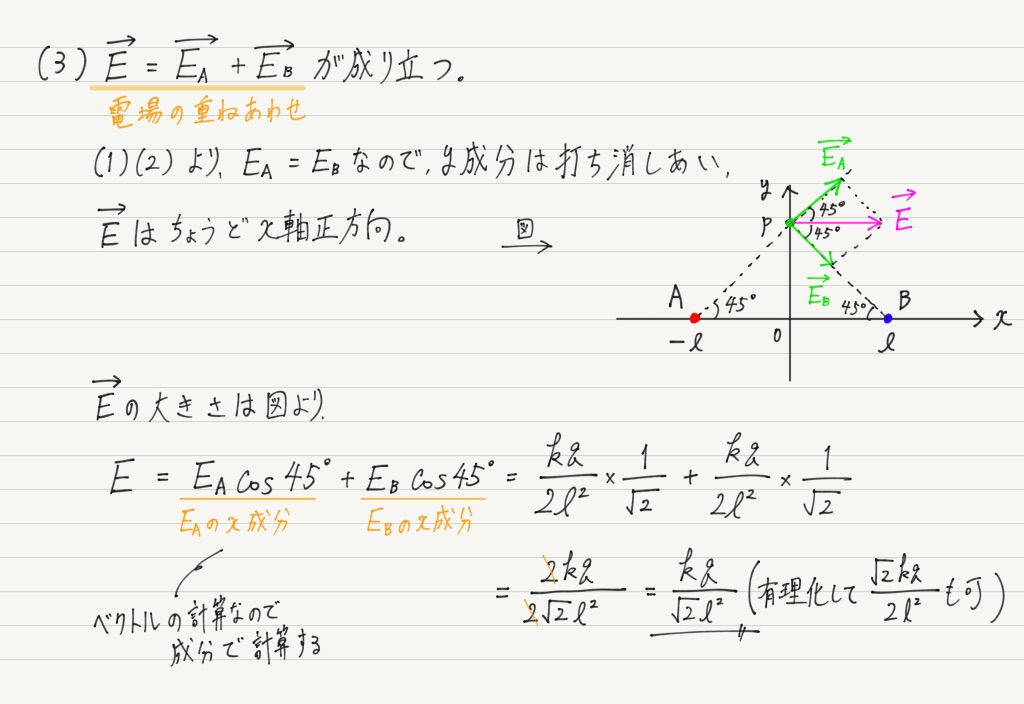
さて，（3）はヒントを差し上げましょう。 点電荷が複数ある場合，ある地点での電場は，それぞれの点電荷がその地点につくる電場を足し合わせたもの（電場の重ねあわせ）になります。 解答はこの下にあるので，解き終わったら答え合わせしましょう！
電場を足すときは大きさどうしを足すのではなく，ベクトルとして足さなければいけないことに注意してくださいね！！
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
実はこれらの力に対しても，電場と同様に，目には見えない磁場や重力場というものがあり，それらが力を及ぼしていると考えられています。 世界は “場” に満ちている…？
次回予告
電場という概念はとても便利なものです！ そんな電場をもっと活用するためのツールを次回学びましょう！
