落下運動のラストを締めくくるのは斜方投射！ 前回の水平投射の考え方をもとにして話を進めていきたいので，未読の方はまずこちらに目を通してください。
さて，斜方投射とはその名の通り，斜め上に向かって物体を放り投げる運動のことです。 学校のスポーツテストでやるボール投げ（遠投）を思い浮かべながら読むと理解が深まるかも？
やっぱり成分に分けて考える
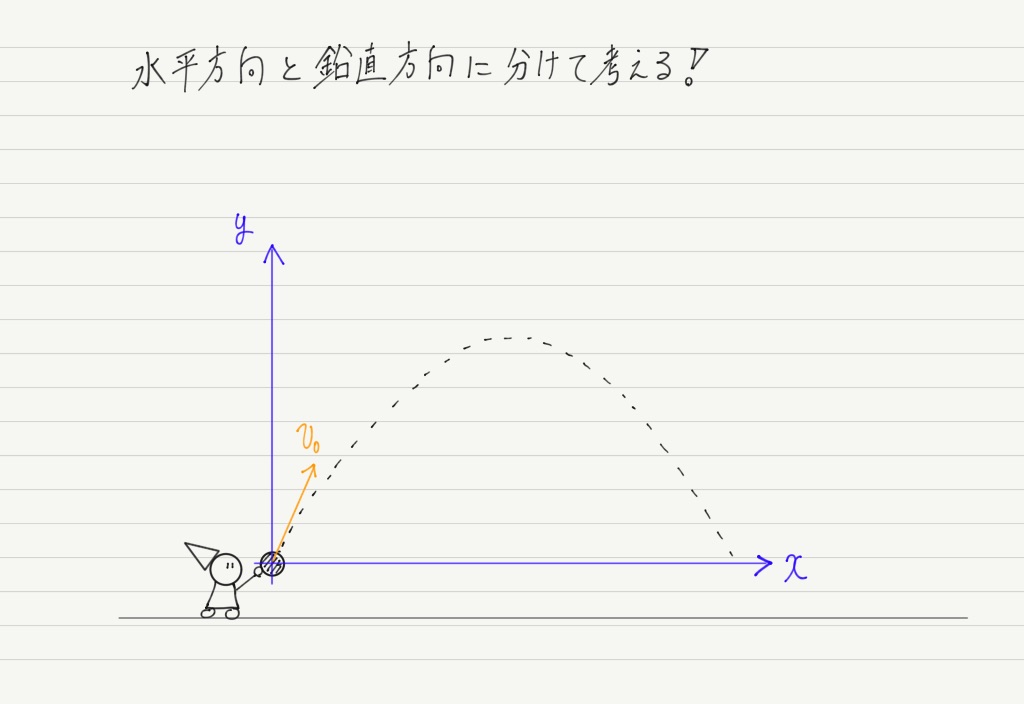
まずボールを斜め上に向かって投げたときの軌道を思い浮かべてください。 ボールは下の図のような曲線運動をしますね？ 曲線運動では，成分に分けて考えるのでした！（水平投射と同じ！）
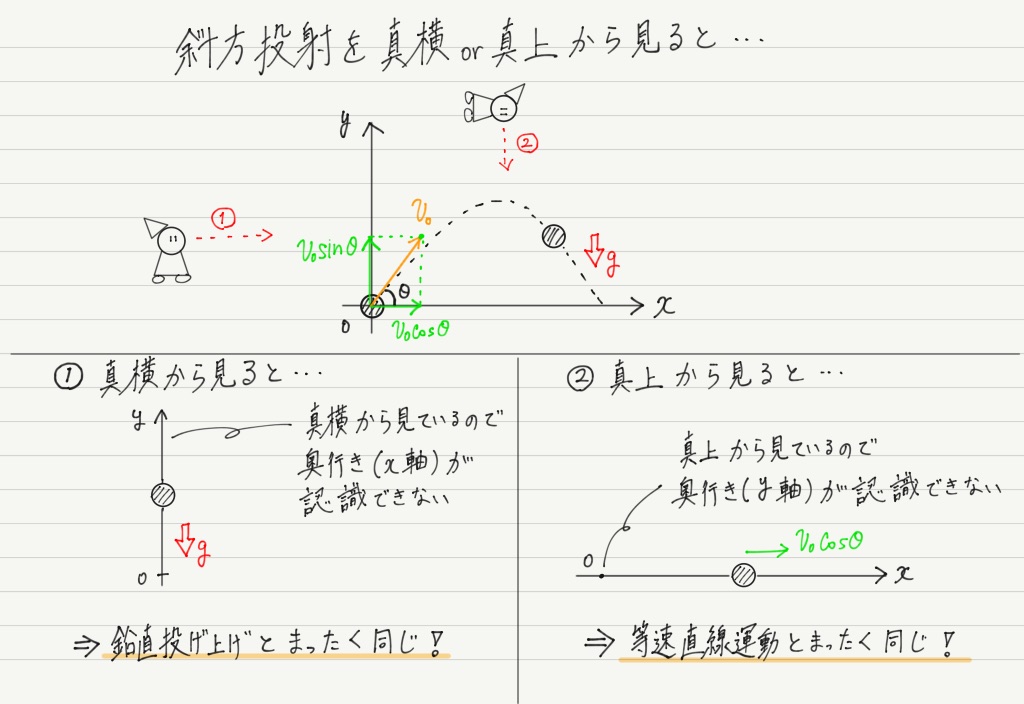
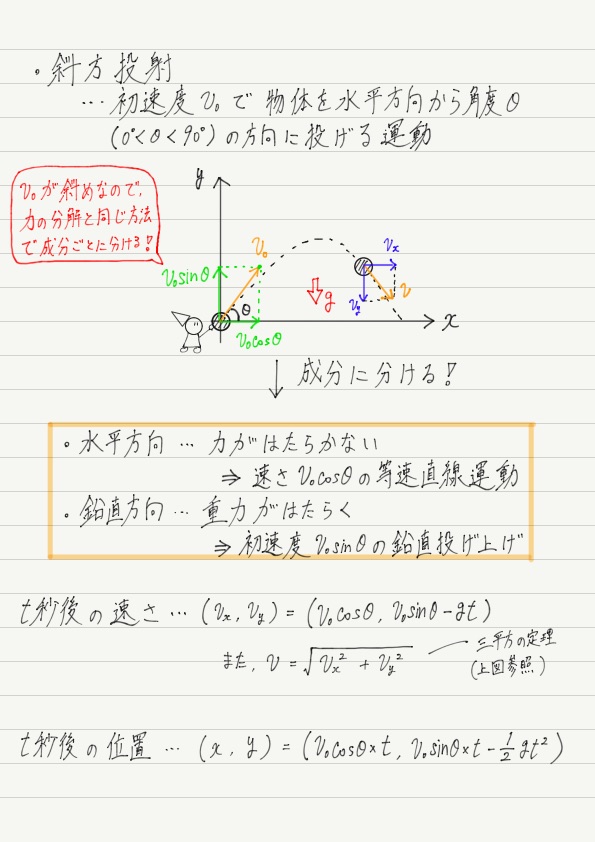
では水平方向（x方向）と鉛直方向（y方向）のそれぞれでどんな運動をするのか調べてみましょう。 水平投射とちがって，今回は初速度も斜め方向なので，それも成分に分ける必要があることに注意してください。
水平投射は自由落下と等速直線運動の組み合わせでしたが，斜方投射は鉛直投げ上げと等速直線運動の組み合わせであることがわかります。
投げ上げと等速直線運動なら，これまで習った知識で問題も解けそうですね！
ただ，例題に入る前に，ちょっとだけ寄り道してみましょう。
ボールの軌道は本当に放物線なのか
「打球は大きな放物線を描いてライトスタンドへー！！」
…など，飛んでいく物体に対して「放物線を描く」という表現はよく用いられます。 一方，放物線という言葉は，数学では2次関数のグラフの概形を指す言葉として登場します。
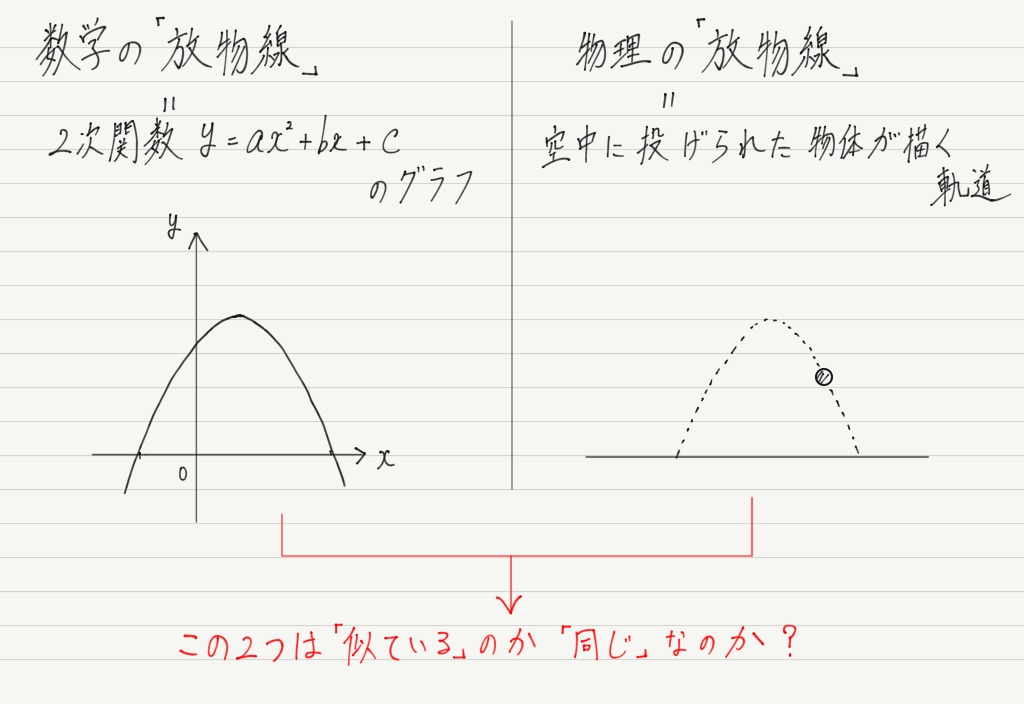
ここで単純な疑問。 斜方投射された物体の描く軌道は，本当に2次関数のグラフと同じなのでしょうか？
ボールの軌道と2次関数のグラフ，「似ている」ことは確かですが，「完全に一致する」かどうかまではちょっとわかりませんよね？
先ほどの「斜方投射＝投げ上げ＋等速直線運動」を使ってこの問題を解決してみましょう！
ボールの軌道，つまりボールが通過する「位置」を調べれば良さそうなので，ボールのx座標とy座標に注目します。
次に，このx座標とy座標の関係を知りたいので，2つの式を連立しましょう。
文字式を連立せよ，と言われると混乱する人がいますが，「連立＝文字を1つ消すこと」ですよ！！
ただし！ 消せるのはもちろん2式に共通している変数だけですよ！
中学校の数学では2つある共通変数xとyのどちらを消してもOKでしたが，今回は共通変数はt のみ。 よって自動的にtを消すことになります。
…これでyとxの関係式が得られました。 まだ見づらいという人のためにもうちょっと工夫してみましょう。
これで最初の疑問がハッキリしました。 斜方投射された物体の描く軌道は，紛れもなく（上に凸の）2次関数のグラフそのものです！！
「似ている」とかのレベルじゃなく「厳密に一致」というのは驚きじゃないですか？？
（空気抵抗などを一切無視すれば，ですが）
数学は空想の産物ではなく，自然界のあちこちにその姿を現しているということを実感してもらえればと思います。
例題
最後に例題をやっておしまいにしましょう。
まず自力で解いてみてください。 三角関数の知識がないと解ききるのは難しいかもしれませんが，やれるところまでやってみましょう。
では，解答です。
解答の途中ですが，いくつか注意事項。
（1）では最高点の速度に注目していますが，斜方投射の場合，速度の鉛直成分だけが0になります。 物体は水平方向には等速直線運動をしているので，最高点であっても水平方向には運動し続けています。
（2）では「最高点までの時間＝最高点から地面までの時間」という関係（運動の対称性）を用いています。
使わなくても答えを求めることは可能ですが，知っていたほうが簡単に解けるし便利です。 知らなかったという人は，物理基礎の鉛直投げ上げの記事を読んでください。
また，最後にsinの2倍角の公式を用いていますが，これを使わないと（3）が解けません。 数学でまだ習っていないという人は「ああ，こういう公式もあるんだ」ぐらいに思ってください（笑）
では，（3）の解説もどうぞ。
「ボール投げは45°で投げると一番遠くまで飛ぶ」というのは直感的に明らかですが，この例題の（3）でそれが数学的に証明されたことになります。
ところで，ボール投げだと45°を意識する人が多いのに，走り幅跳びだと意識しない人が多いのは何でだろう…？
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
物理基礎から長らく続いた落下運動の話はこれにて終了。 次回からは完全に新しい内容に入ります！
