前回の記事では音源が動く場合のドップラー効果について解説しましたが,今回は「観測者が動く場合のドップラー効果」を見ていくことにしましょう!
同じ現象なのにちがう原因!?
前回の結論,「音源が観測者に近づくと,音は実際より高く聞こえる(振動数が大きくなる)」をまず思い出してください。
今回はその逆で,静止した音源に対して,観測者が近づく場合を考えます。
で,結論を先に言っちゃうと,音は実際より高く聞こえるのです。
そして,ドップラー効果を理解する上での落とし穴がここに潜んでいます。
「音源が観測者に近づく」と「観測者が音源に近づく」という似た現象で,「音が高く聞こえる」という同じ結論が出ているので,原因も同じだと考えがちです。
ところが,この2つの現象は結論に至るまでのプロセスがまったくちがいます!!
同じ結論だからといって,原因も同じとは限りません。
何がどうちがうのか,さっそく解説していきます!
ベルトコンベアー再び
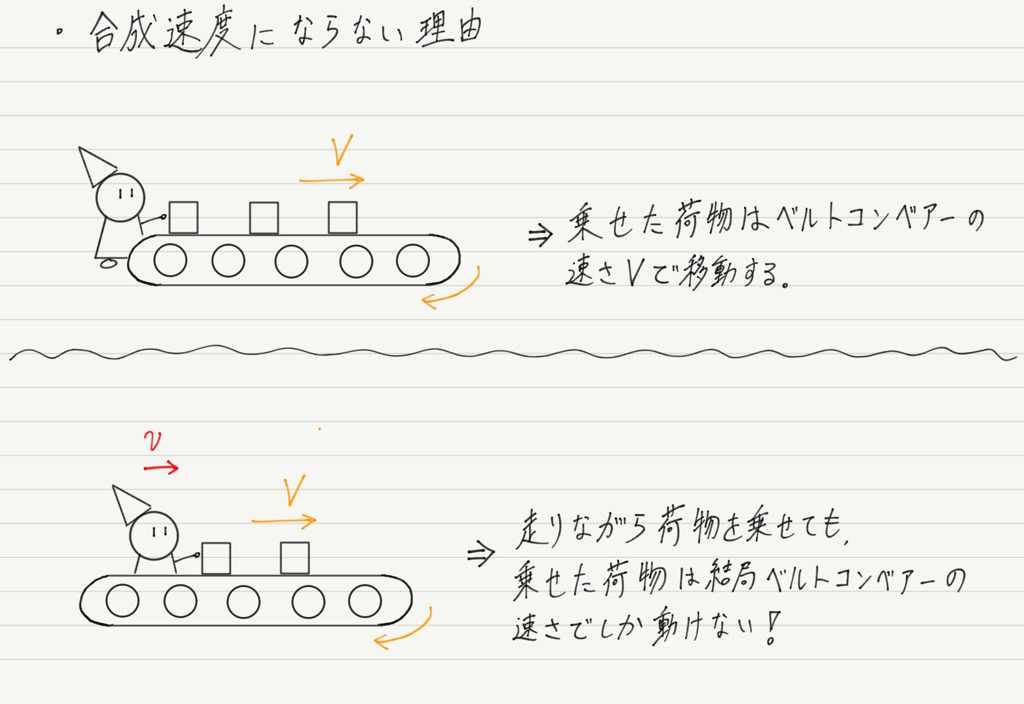
前回,音源が動く場合の様子をベルトコンベアーに例えました。
ポイントは,「走りながら荷物を乗せても,乗せた後の速さはベルトコンベアーの速さで決まる」ということでした。
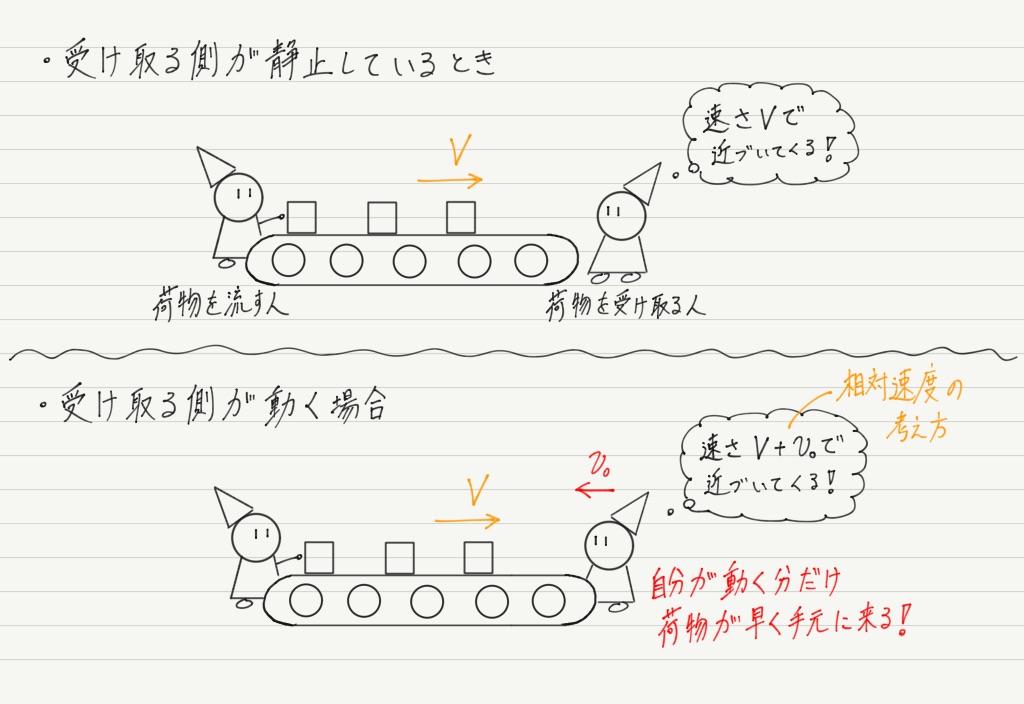
さて,今回は観測者に焦点を当てたいので,ベルトコンベアーを流れる荷物を受け取る人を考えましょう。
流れてきた荷物を3つ受け取る場合,流れてくるのをじっと待つよりも,自ら荷物に近づいていったほうがすばやく回収できます。
…まぁ,当たり前ですよね笑
当たり前なんですが,音源が動く場合とのちがいが大事。
「荷物を流す人(=音源)が動いても,荷物の速度には影響を与えない」のに対し,「荷物を受け取る人(=観測者)が動くと,観測者から見た荷物の相対速度が変化する」のです!
観測者が近づく場合の考察
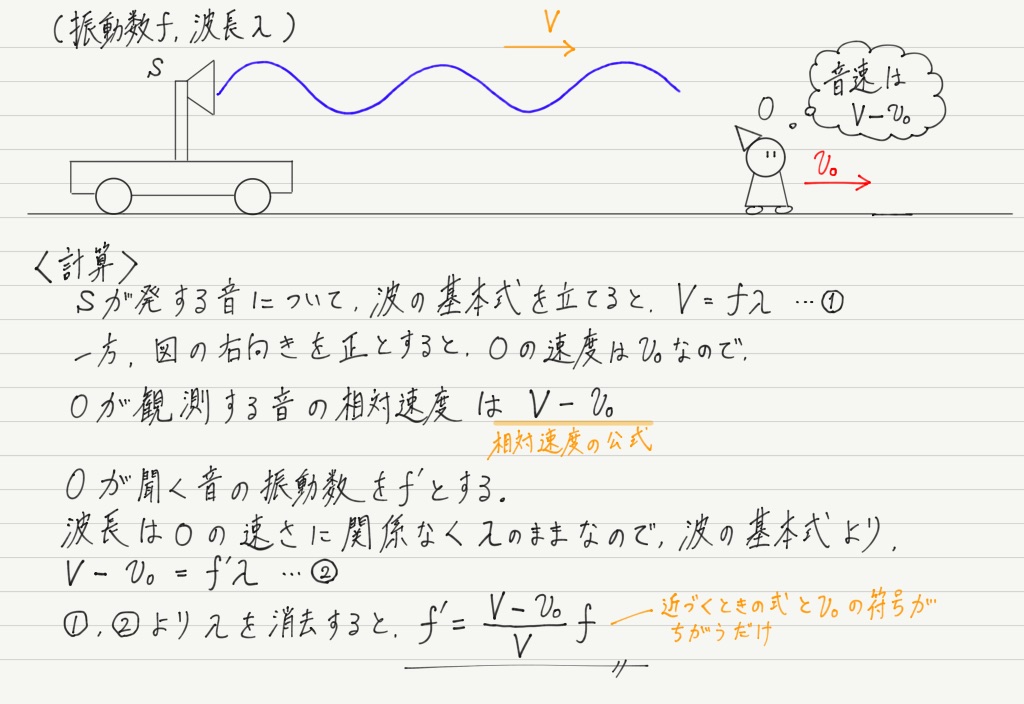
動く観測者からは音速が変化して見えるというのが,今回の最大のポイントになります。
それからもうひとつ。 観測者が動いても音の波長は変化しません!
ベルトコンベアーの例だと「波長=荷物と荷物の間隔」ですが,間隔は荷物を置いたときに決まるので,観測者が止まっていようが動いていようが変化しません。
このことを念頭に置いて,さっそく計算してみましょう。
これが観測者が近づく場合のドップラー効果の式です!
分子が分母より大きくなっているので,f’ がf より大きい(=音が実際より高く聞こえる)ことが式から読み取れます。
観測者が遠ざかる場合の考察
同様に観測者が遠ざかる場合も計算できます。 この場合も運動の向きに注意して相対速度を考えればOK。
さっきは音に向かって運動していたので,相対速度は元の速度より大きくなりましたが,今回は音から離れる方向に運動するので,相対速度は元の速度より小さくなります!
今度は分子が分母より小さくなっているので,f’ がf より小さい(=音が実際より低く聞こえる)ことがわかります。
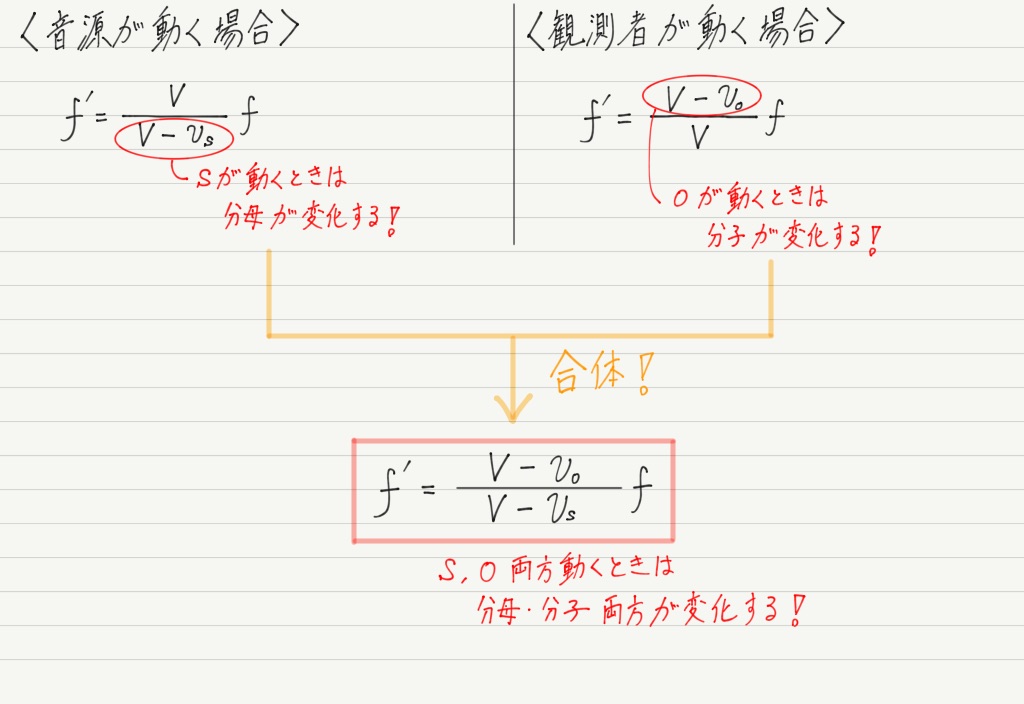
ドップラー効果の式【完全ver.】
音源が動く場合と観測者が動く場合の式が出揃いましたが,問題によっては「両方動く場合」もあったりするので,2つの式を合体させて1つにしておきましょう!
注意点は,近づく場合と遠ざかる場合で符号が変わる場所があるということです。
音源が近づく or 遠ざかる,観測者が近づく or 遠ざかる,の4パターンしかないのでそれぞれ暗記しても結構ですが,音の向きを基準にして符号を決めることもできます!
ただ,前回も言いましたが,ドップラー効果は振動数の式だけではなく,そこに至るまでの道筋が重要。
自力で式が導けるようになっていれば,テスト中に「あれ?どっちが分母だっけ?」「符号はどっちだっけ?」となったときでもちゃんと対応できるはずです。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
高校物理の波は,音と光の2本立てですが,音はこれにて終了。 次回からは満を持して光に突入します!!